
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Левосторонний и правосторонний пределы функции в точкеПереходим к рассмотрению односторонних пределов функции в точке x0, при которых переменная x «движется» к x0 слева (левосторонний предел) или справа (правосторонний предел). Нам потребуется понятие полуокрестности. Пусть d > 0. Интервал (a, x0) называется левой полуокрестностью точки x0, интервал (x0 – d, x0) – левой d-полуокрестностью точки x0. Интервалы (x0, b), (x0, x0 + d) называются, соответственно, правой полуокрестностьюи правойd-полуокрестностью точки x0 (см. рис. 1.8, 1.9).
Пусть f(x0) определена в левой полуокрестности точки x0. Число b называется левосторонним пределом функции f(x) в точке x0 (обозначение: Символически Аналогично, число b называется правосторонним пределом функции f(x) в точке x0 (обозначение: Символически
f(x) = Найти Решение. Покажем, что Рассмотрим значения x < 1, тогда f(x) = 2x – 1 и | f(x) – 1| = |2x – 1 – 1| = 2|x – 1|. Зафиксируем малое e > 0. Подсчитаем: | f(x) – 1| < e Û 2 |x – 1| < e Û |x – 1| < Рассмотрим значения x > 1, тогда f(x) = 4 – x. Зафиксируем e > 0,  | f(x) – 3| = |2 – x – 3| = |1 – x|. Отсюда | f(x) – 1| < e Û |1 – x| < e, т.е. | f(x) – 1 | < e для Очевидно, если Верно и обратное, если Если же правосторонний предел функции в точке x0 не равен левостороннему пределу функции в точке x0, то |
|||||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 395. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 f(x) = b), если для любого e > 0 найдется d > 0, такое, что для всех значений x, принадлежащих левой d-полуокрестности (x0 – d, x0), выполняется неравенство:
f(x) = b), если для любого e > 0 найдется d > 0, такое, что для всех значений x, принадлежащих левой d-полуокрестности (x0 – d, x0), выполняется неравенство:  f(x) = b означает: "e>0$d > 0 "x(x0 – d < x < x0 ® | f(x) – b | < e) (см. рис. 1.8).
f(x) = b означает: "e>0$d > 0 "x(x0 – d < x < x0 ® | f(x) – b | < e) (см. рис. 1.8). f(x) = b), если для любого e > 0 найдется d > 0, такое, что для всех значений x, принадлежащих правой d-полуокрестности (x0, x0 + d), выполняется неравенство: | f(x) – b | < e (см. рис. 1.9).
f(x) = b), если для любого e > 0 найдется d > 0, такое, что для всех значений x, принадлежащих правой d-полуокрестности (x0, x0 + d), выполняется неравенство: | f(x) – b | < e (см. рис. 1.9). Пример 3. Функция f(x) задана равенством (рис. 1.10):
Пример 3. Функция f(x) задана равенством (рис. 1.10):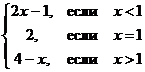 .
. f(x) и
f(x) и  f(x).
f(x).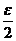 . Так как x < 1, то
. Так как x < 1, то 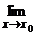 f(x) = b, то
f(x) = b, то