
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основные теоремы о пределахТеорема 1. Если Доказательство.Пусть Из определения Итак, из равенства a(x) = f(x) – b имеем f(x) = b + a(x), где a(x) – б.м. при x ® +¥. Теорема 2. Если функцию f(x) можно представить в виде: f (x) = b + a(x), где Доказательство. Пусть f(x) = b + a(x), где a(x) – б.м. при x ® +¥, т.е. "e > 0 $x0 "x > x0 |a(x)| < e. (*) Но a(x) = f (x) – b, поэтому (*) можно записать так: "e > 0 $x0 "x > x0 |f (x) – b| < e, что означает: Следующие теоремы значительно облегчают нахождение пределов. Теорема 3. Предел суммы (разности) двух функций равен сумме (разности) их пределов, т.е. если
Доказательство. На основании теоремы 1: f1(x) = b1 + a1(x), f2(x) = b2 + a2(x), где a1(x), a2(x) – б.м. при x ® a, тогда f1(x) + f2(x) = (b1 + a1(x)) + (b2 + a2(x)) = (b1 + b2) + (a1(x) + a2(x)). Но a1(x) + a2(x) – б.м. функция при x ® a (как сумма двух б.м. функций), поэтому из равенства f1(x) + f2(x) = (b1 + b2) + (a1(x) + a2(x)) по теореме 2 следует, что
Аналогично проводится доказательство для разности. Теорема 4. Предел произведения двух функций равен произведению их пределов, т.е. если Доказательство.По теореме 1: f1(x) = b1 + a1(x), f2(x) = b2 + a2(x), где a1(x), a2(x) – б.м. при x ® a, тогда f1(x)× f2(x) = b1× b2 + b1×a2(x) + b2×a1(x) + a1(x)× a2(x). На основании следствий 2, 3, теоремы 1 (разд. 1.6) функции b1×a2(x), b2×a1(x), a1(x)×a2(x) – б.м. при x ® a и a(x) = b1×a2(x) + b2×a1(x) + a1(x)×a2(x) – бесконечно малая функция при x ® a. Из равенства f1(x) f2(x) = b1b2 + a(x) по теореме 2 следует, что  Следствие 1. Постоянный множитель можно выносить за знак предела, т.е. Доказательство. Следствие 2. Если n – натуральное число, то Теорема 5. Предел дроби равен пределу числителя, деленному на предел знаменателя при условии, что предел знаменателя не равен нулю. Иначе, если Доказательство.По теореме 1: f1(x) = b1 + a1(x), f2(x) = b2 + a2(x), где a1(x), a2(x) – б.м. при x ® a, тогда
Обозначим последнюю дробь a(x) = Рассмотрим применение доказанных теорем при нахождении пределов. Пример. Найти Решение. Найдем сначала предел числителя и знаменателя. По свойствам пределов
Теорема 6. Если Доказательство. Пусть Теорема 7. Если "x (f1(x) ³ f2(x)) и Доказательство. Рассмотрим функцию F(x) = f1(x) – f2(x), тогда "x (F (x) ³ 0) и Теорема 8. (теорема о сжатой переменной). Если "x (f1(x) £ j(x) £ f2(x)) и
Пусть Покажем, что "xÎ(x0, x0 + d1) |f1(x) – b| < e, и найдется такое d2 > 0, что "xÎ(x0, x0 + d2) |f2 (x) – b| < e. Обозначим через d меньшее из d1, d2, тогда для xÎ(x0, x0 + d) эти неравенства будут выполняться одновременно. Преобразуем их, используя определение модуля: "xÎ(x0, x0 + d) (b – e < f1(x) < b + e), "xÎ(x0, x0 + d) (b – e < f2(x) < b + e). И учтем данное неравенство: f1(x) £ j(x) £ f2(x). Тогда из этих неравенств получим: b – e < f1(x) £ j(x) £ f2(x) < b + e, откуда |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 343. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
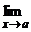 f(x) = b, то f(x) = b + a(x), где a(x) – б.м. при x ® a.
f(x) = b, то f(x) = b + a(x), где a(x) – б.м. при x ® a. f (x) = b. Рассмотрим функцию a(x) = f(x) – b и покажем, что a(x) – б.м. при x ® +¥ .
f (x) = b. Рассмотрим функцию a(x) = f(x) – b и покажем, что a(x) – б.м. при x ® +¥ .
 .
.
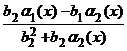 , тогда
, тогда  + a(x). Остается показать, что a(x) – б.м. при x ® a. Действительно, числитель дроби
+ a(x). Остается показать, что a(x) – б.м. при x ® a. Действительно, числитель дроби  – функция,ограниченная при x ® a (по теореме 3 разд. 1.6). Значит, a(x) – б.м. при x ® a (по теореме 4 разд. 1.6). Теорема доказана.
– функция,ограниченная при x ® a (по теореме 3 разд. 1.6). Значит, a(x) – б.м. при x ® a (по теореме 4 разд. 1.6). Теорема доказана. .
. 3 x = 3
3 x = 3 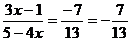 .
. . Докажем методом от противного, предполагая, что
. Докажем методом от противного, предполагая, что  f(x) = b< 0. Зафиксируем e = –
f(x) = b< 0. Зафиксируем e = – 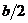 , e > 0. По определению предела по e найдется x0, такое, что "x > x0 |f(x) – b| < e, отсюда b – e < f (x) < b + e. Но e = –
, e > 0. По определению предела по e найдется x0, такое, что "x > x0 |f(x) – b| < e, отсюда b – e < f (x) < b + e. Но e = –  Доказательство
Доказательство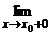 f1(x) =
f1(x) =