
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема 2 (второй замечательный предел)Существует предел Доказательство. Рассмотрим последовательность
Покажем, что эта последовательность возрастающая и ограниченная. Для этого воспользуемся формулой бинома Ньютона:
Преобразуем по этой формуле
В полученном выражении: третье слагаемое четвертое и т.д., а последнее Получаем:
Покажем, что последовательность
Так как Покажем, что последовательность Если в равенстве (**) каждую из скобок
Так как
По формуле суммы геометрической прогрессии имеем:
Последовательность
Так как 2 < an < 3, то 2 < Число e широко используется как основание для показательной функции Рассмотрим (рис. 1.13) функцию y =
Нетрудно показать, что
Все записанные пределы объединяются одним названием второго замечательного предела.  Рассмотрим применение второго замечательногопредела для вычисления некоторых пределов. Пример.Найти Решение. Обозначим: 3n = m, n =
Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции Пусть a(x) и b(x) – б.м. функции при x ® a (x® + ¥, x ® –¥, x ® x0, ...). Рассмотрим предел их отношения при x ® a. 1. Если 2. Если 3. Если a(x) – б.м. высшего порядка, чем b(x), и 4. Если не существует 5. Если Пример 1. a(x) = (1 – x)3, b (x) = 1 – x3. Очевидно, что при x ® 1 функции a(x), b(x) являются б.м. Для их сравнения найдем предел их отношения при x ® 1:
Вывод: a(x) является б.м. высшего порядка, по сравнению с b(x) при x ® 1. Нетрудно убедиться, что Пример 2. Функции a1(x) = 4x, a2 (x) = x2, a3(x) = sinx, a4(x) = tgx являются бесконечно малыми при x ® 0. Сравним их:
Отсюда заключаем, что a2(x) = x2 – б.м. высшего порядка, по сравнению с a1(x) и a3(x) (при x ® 0), a1(x) и a3(x) – б.м. одного порядка, a3(x) и a4(x) – эквивалентные б.м., т.е. sinx ~ tgx при x ® 0. Теорема 1. Пусть a(x) ~ a1(x), b(x) ~ b1(x) при x ® a. Если существует Доказательство.
Эта теорема позволяет упрощать нахождение пределов. Пример 3. Найти В силу первого замечательного предела sin4x ~ 4x, tg3x ~ 3x при x ® 0, поэтому
Теорема 2. Бесконечно малые функции a(x) и b(x) эквивалентны (при x ® a) тогда и только тогда, когда a(x) – b(x) является б.м. высшего порядка, по сравнению с a(x) и b(x) (при x ® a). Доказательство Пусть a(x) ~ b(x) при x ® a. Тогда Пусть a(x) – b(x) – б.м. высшего порядка, по сравнению с a(x) и b(x), покажем, что a(x) ~ b(x) при x ® a:
т.е. a(x) ~ b(x) при x ® a. Теорема 3. Сумма конечного числа бесконечно малых различных порядков эквивалентна слагаемому низшего порядка. Доказательство. Пусть a(x) – б.м. низшего порядка по сравнению с b(x) и g(x) при x ® a, т.е. Покажем, что a(x) ~ (a(x) + b(x) + g(x)) при x ® a:
Доказанные теоремы применяются для нахождения пределов. Пример 4. Найти По теореме 3 при x ® 0: 4x + 2x3 ~ 4x , sin2x + 3tg5x + x3 ~ 3tg5x, тогда
|
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 385. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
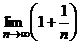 .
. с общим членом
с общим членом 
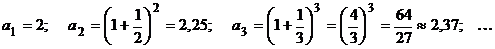
 .
.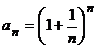 , полагая
, полагая  :
: .
.
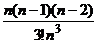 =
= 

 (*)
(*) возрастающая, т.е.
возрастающая, т.е. 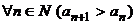 :
:
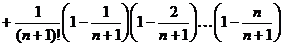 (**)
(**) то
то  и т.д., поэтому каждое слагаемое (начиная с третьего) из равенства (*) меньше соответствующего слагаемого из равенства (**), кроме того, в равенстве (**) правая часть содержит на одно (положительное) слагаемое больше. Отсюда заключаем, что
и т.д., поэтому каждое слагаемое (начиная с третьего) из равенства (*) меньше соответствующего слагаемого из равенства (**), кроме того, в равенстве (**) правая часть содержит на одно (положительное) слагаемое больше. Отсюда заключаем, что  .
.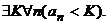
 заменить на 1 (на большее число), то получим неравенство:
заменить на 1 (на большее число), то получим неравенство:

 то
то .
. поэтому
поэтому  .
. возрастает и ограничена сверху, по теореме 1 существует предел, этот предел называют неперовым числом и обозначают через e. Итак,
возрастает и ограничена сверху, по теореме 1 существует предел, этот предел называют неперовым числом и обозначают через e. Итак,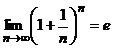 .
.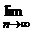 an
an 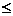 3, т.е. 2 < e
3, т.е. 2 < e  2,718282.
2,718282. (экспонента) и как основание для логарифмов
(экспонента) и как основание для логарифмов  (натуральные логарифмы).
(натуральные логарифмы). , которая не определена на отрезке
, которая не определена на отрезке  (подумайте почему?). Ее область определения (–
(подумайте почему?). Ее область определения (– 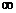 , –1)
, –1)  (0, +
(0, +  Известно, что
Известно, что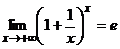 и
и  .
. .
.
 . Если n
. Если n 
 и мы получим:
и мы получим: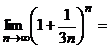
 =
= 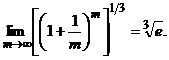
 = b и b – конечное число, b ¹ 0, то функции a(x), b(x) называются бесконечно малыми одного порядка малости при x ® a.
= b и b – конечное число, b ¹ 0, то функции a(x), b(x) называются бесконечно малыми одного порядка малости при x ® a.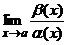 = ¥.
= ¥. = b ¹ 0 (b – конечное число, k Î N), то a(x) называют бесконечно малой k-го порядка, по сравнению с b(x) при x ® a.
= b ¹ 0 (b – конечное число, k Î N), то a(x) называют бесконечно малой k-го порядка, по сравнению с b(x) при x ® a. (ни конечный, ни бесконечный), то a(x), b(x) называют несравнимыми б.м. при x ® a.
(ни конечный, ни бесконечный), то a(x), b(x) называют несравнимыми б.м. при x ® a. =
= 
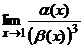 =
=  (убедитесь!), откуда следует, что a(x) – б.м. 3-го порядка малости, по сравнению с b(x) при x ® 1.
(убедитесь!), откуда следует, что a(x) – б.м. 3-го порядка малости, по сравнению с b(x) при x ® 1.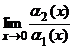 = 0,
= 0,  ,
,  = 1,
= 1,  = ¥.
= ¥. , то существует и
, то существует и 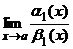 .
.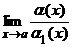 = 1,
= 1,  = 1,
= 1, =
= 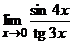 .
. =
=  .
. =
=  = 0, т.е. разность a(x) – b(x) – б.м. высшего порядка, по сравнению с a(x) при при x ® a (аналогично с b(x)).
= 0, т.е. разность a(x) – b(x) – б.м. высшего порядка, по сравнению с a(x) при при x ® a (аналогично с b(x)). =
=  +
+  = 1,
= 1,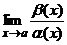 = 0 и
= 0 и  = 0.
= 0. =
=  +
+  .
. =
= 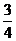
 =
=  .
.