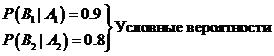Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дифференциальное преобразование случайных функций.Дана случайная функция X(t) с математическим ожиданием mx(t) и корреляционной функцией Кx(t, t'). Случайная функция Y(t) связана со случайной функцией X(t) линейным однородным оператором дифференцирования: Требуется найти my(t) и Кy(t, t’). Представим производную в виде предела: è my(t) = M[Y(t)] = т. е. математическое ожидание производной от случайной функции равно производной от ее математического ожидания. Для определения Ky(t, t’) перейдем к центрированным случайным функциям Y(t) и X(t); очевидно, По определению Ky(t, t’) = M[ è Ky(t, t’) = Итак, чтобы найти корреляционную функцию производной, нужно дважды продифференцировать корреляционную функцию исходной случайной функции: сначала по одному аргументу, затем — по другому. Если случайная функция X(t) с математическим ожиданием mx(t) и корреляционной функцией Kx(t, t') преобразуется линейным однородным оператором L в случайную функцию Y(t) = L{X(t)}; то для нахождения математического ожидания случайной функции Y(t) нужно применить тот же оператор к математическому ожиданию случайной функции X(t): my(t) = L{mx(t)} а для нахождения корреляционной функции нужно дважды применить тот же оператор к корреляционной функции случайной функции X(t), сначала по одному аргументу, затем — по другому: Ky(t, t’) = L(t)L(t'){Kx(t, t’)} Дисперсию Dy (t) можно найти, зная корреляционную функцию: Dy (t) = Ky(t, t).
Задача 4.16 Для получения небрака: +) В первой технологии: +) Во второй технологии: Но
Экзаменационный Билет №31 |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 231. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

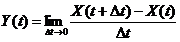

 (t)=
(t)= 
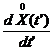 ] =
] =