
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Нормальная функция распределения вероятности. Интеграл вероятности.Найдем функцию распределения F(x) случайной величины X, распределенной по нормальному закону с параметрами m, σ. Плотность распределения величины X равна:
Математическое ожидание: mx=m, а дисперсия Dx=σ2. Отсюда находим функцию распределения: F(x) = Сделаем замену переменной: Интеграл не выражается через элементарные функции, но его можно вычислить через специальную функцию, выражающую определенный интеграл от выражения Условимся называть функцию Выразим функцию распределения величины X с параметрами m и σ через нормальную функцию распределения: F(x) = Теперь найдем вероятность попадания случайной величины X на участок от α до β. Согласно формуле: P(α<x<β) =
Применение центральной предельной теоремы. а) Пусть Предположим, что условия центральной предельной теоремы выполнены и число слагаемых п достаточно для того, чтобы закон распределения величины Тогда вероятность того, что случайная случайная величина У попадает в пределы участка
Где Ф* — нормальная функция распределения. b) Частным случаем центральной предельной теоремы для дискретьых случайных величин является теорема Лапласа. Если производится п независимых опытов, в каждом из которых событие А появляется с вероятностью р, то справедливо соотношение 
где Y — число появлений события А в n опытах, q = l — р.
Задача 15.7 Экзаменационный Билет №27 Закон Пуассона. Дискретная случайная величина X называется распределенной по закону Пуассона, если ее возможные значения 0,1,2,..., m, ..., а вероятность того, что X = m, выражается формулой
где а > 0 — параметр закона Пуассона. Математическое ожидание и дисперсия случайной величины X, распределенной по закону Пуассона, равны параметру закона а: mx = а = Dx . для вычисления вероятности Рm, n того, что событие А появится ровно m раз, можно воспользоваться приближенной формулой
О парной и групповой зависимости случайных событий. Несколько событий называют попарно независимыми, если каждые два из них независимы. Например, события А, В, С попарно независимы, если независимы события А и В, А и С, В и С. События
Если события Подчеркнем, что если несколько событий независимы попарно, то отсюда еще не следует их независимость в совокупности. В этом смысле требование независимости событий в совокупности сильнее требования их попарной независимости. Задача 31.10
Экзаменационный Билет №28 |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 187. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


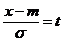 и приведем его к виду: F(x) =
и приведем его к виду: F(x) = 
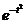 или
или  (так называемый интеграл вероятностей), для которого составлены таблицы.
(так называемый интеграл вероятностей), для которого составлены таблицы. нормальной функцией распределения.
нормальной функцией распределения.
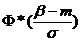 -
- 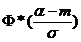
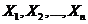 — независимые случайные величины с математическими ожиданиями
— независимые случайные величины с математическими ожиданиями 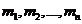 и дисперсиями
и дисперсиями 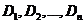
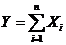 можно было считать приближенно нормальным.
можно было считать приближенно нормальным.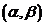 , выражается фопмулой
, выражается фопмулой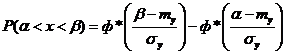
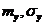 математическое ожидание и среднее квадратическое отклонение величины V,
математическое ожидание и среднее квадратическое отклонение величины V,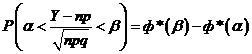
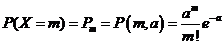

 называются независимыми в совокупности, если для любого
называются независимыми в совокупности, если для любого  и любого набора различных меж собой индексов
и любого набора различных меж собой индексов  имеет место равенство:
имеет место равенство:
 независимы. Достаточно в равенстве
независимы. Достаточно в равенстве  взять
взять 
