Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Линейные преобразования случайных функций.Пусть на вход линейной системы с оператором L воздействует случайная функция X (t), причем известны ее характеристики: математическое ожидание mx(t) и корреляционная функция Kx(t, t'). Реакция системы представляет собой случайную функцию Y(t) = L(X(t)). Требуется найти характеристики случайной функции Y(t) на выходе системы: my(t) и Ky(t, t'). Короче: по характеристикам случайной функции на входе линейной системы найти характеристики случайной функции на выходе. Покажем сначала, что можно ограничиться решением этой задачи только для однородного оператора L. Действительно, пусть оператор L неоднороден и выражается формулой: L(X(t)) = L0(X(t))+ρ(t). где L0—линейный однородный оператор, ρ(t)— определенная неслучайная функция. Тогда my(t) = M[L0{X(t)}] + ρ(t). т. е. функция ρ(t) просто прибавляется к математическому ожиданию случайной функции на выходе линейной системы. Что же касается корреляционной функции, то, как известно, она не меняется от прибавления к случайной функции неслучайного слагаемого. Поэтому в дальнейшем изложении под «линейными операторами» будем разуметь только линейные однородные операторы. Решим задачу об определении характеристик на выходе линейной системы сначала для некоторых частных видов линейных операторов. Первое обобщение схемы независимых испытаний. Пусть производится n независимых опытов, в каждом из которых может появиться или не появиться некоторое событие А, причем вероятность появления события А в i-м опыте равна pi, а вероятность непоявления qi=1 – pi(i= 1...n). Требуется найти вероятность Рm,n того, что в результате n опытов событие А появится ровно m раз.  Вероятность того, что событие А в n независимых опытах появится ровно m раз, равна коэффициенту при xm в выражении производящей функции:
где pi — вероятность появления события А в i-м опыте, qi = 1 – pi
Задача 32.9
Экзаменационный Билет №25 О замечательных свойствах законов Пуассона, показательного и нормального з.р.в.
Функция распределения случайной величины Для случайной величины Т, распределенной по показательному закону mt=1/α; Dt=1/α2. 2.Первое и второе обобщение схемы независимых испытаний. 1. Пусть производится n независимых опытов, в каждом из которых может появиться или не появиться некоторое событие А, причем вероятность появления события А в i-м опыте равна pi, а вероятность непоявления qi=1 – pi(i= 1...n). Требуется найти вероятность Рm,n того, что в результате n опытов событие А появится ровно m раз. Вероятность того, что событие А в n независимых опытах появится ровно m раз, равна коэффициенту при xm в выражении производящей функции:
где pi — вероятность появления события А в i-м опыте, qi = 1 – pi
2.Пусть производится n независимых опытов, в каждом из которых событие А1 появится m1раз с вероятностью p1 А2 появится m2 раз с вероятностью p2 ...................... Аk появится mk раз с вероятностью pk И Такая вероятность равна коэффициенту при
Задача 7.14 Вероятность попадания при пятом выстреле: Первый случай (стрелок) 0.4; 0.5; 0.45; 0.55; 0.5; Второй случай (стрелок) 0.5; 0.4; 0.55; 0.45; 0.6 То вероятность того, что первым произвел выстрел первый стрелок:
Экзаменационный Билет №26 |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 169. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


 имеет показательное (экспоненциальное) распределение с параметром
имеет показательное (экспоненциальное) распределение с параметром 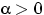 , и пишут:
, и пишут:  , если
, если 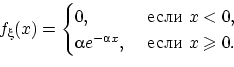

 . Требуется найти вероятность Рn,m1m2,...,mk того, что в результате n опытов событие Аi появится ровно mi раз.
. Требуется найти вероятность Рn,m1m2,...,mk того, что в результате n опытов событие Аi появится ровно mi раз. в выражении производящей функции:
в выражении производящей функции: