
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Интеграл вероятности, его применение для вычисления вероятности попадания на заданный интервал.Найдем функцию распределения F(x) случайной величины X, распределенной по нормальному закону с параметрами m, σ. Плотность распределения величины X равна:
Математическое ожидание: mx=m, а дисперсия Dx=σ2. Отсюда находим функцию распределения: F(x) = Сделаем замену переменной: Интеграл не выражается через элементарные функции, но его можно вычислить через специальную функцию, выражающую определенный интеграл от выражения Условимся называть функцию Выразим функцию распределения величины X с параметрами m и σ через нормальную функцию распределения: Теперь найдем вероятность попадания случайной величины X на участок от α до β. Согласно формуле: Числовые характеристики функции случайных величин. 1- Если X — дискретная случайная величина с рядом распределения
а величина У связана с X функциональной зависимостью
а дисперсиявыражается любой из двух формул
Если (X, Y) — система дискретных случайных величин, распределение которой характеризуется вероятностями
а дисперсиявыражается любой из двух формул
2- Если X — непрерывная случайная величина с плотностью распределения
а дисперсия выражается любой из двух формул
Если (X, У) — система непрерывных случайных величин с плотностью 
а дисперсия выражается любой из двух формул
Если
Задача 18.2.
Экзаменационный Билет №20 Правило 3-х сигм. Пусть имеется нормально распределённая случайная величина x с математическим ожиданием, равным а и дисперсией s2.
Определим вероятность попадания x в интервал (а – 3s; а + 3s), то есть вероятность того, что x принимает значения, отличающиеся от математического ожидания не более, чем на три среднеквадратических отклонения. P(а – 3s< x < а + 3s)=Ф(3) – Ф(–3)=2Ф(3) По таблице находим Ф(3)=0,49865, откуда следует, что 2Ф(3) практически равняется единице. Таким образом, можно сделать важный вывод: нормальная случайная величина принимает значения, отклоняющиеся от ее математического ожидания не более чем на 3s. |
||||||||||||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 200. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


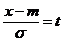 и приведем его к виду: F(x) =
и приведем его к виду: F(x) = 
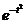 или
или  (так называемый интеграл вероятностей), для которого составлены таблицы.
(так называемый интеграл вероятностей), для которого составлены таблицы. нормальной функцией распределения.
нормальной функцией распределения.

 то матическое ожидание величины У равно
то матическое ожидание величины У равно

 , a
, a  то математическое ожидание величины Z равно
то математическое ожидание величины Z равно

 , а
, а 

 , a
, a 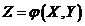 , то математическое ожидание величины Z равно
, то математическое ожидание величины Z равно
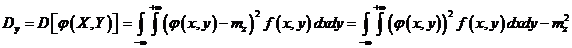
 — система п непрерывных случайных величин с плотностью
— система п непрерывных случайных величин с плотностью  а
а  , то
, то


