
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Показательное ( экспоненциальное ) распределение, его числовые характеристики.
Функция распределения случайной величины
Для случайной величины Т, распределенной по показательному закону mt=1/α; Dt=1/α2.
2. Теоремы о числовых характеристиках: 1- Дисперсия суммы двух случайных величин равна сумме их дисперсий плюс удвоенный корреляционный момент:
Доказательство.
2- Дисперсия линейной функции: где Кij — корреляционный момент величин Хi, Xj. Доказательство. Введем обозначение:
где Вычислим этот момент. Имеем:
Подставляя это выражение в (1), приходим к формуле В частном случае, когда все величины (X1 X2, .... Хn) некоррелированны, то дисперсия линейной функции некоррелированных случайных величин равна сумме произведений квадратов коэффициентов на дисперсии соответствующих аргументов.
3- Математическое ожидание произведения случайных величин равно произведению их математических ожиданий плюс корреляционный момент:
Доказательство.
Математическое ожидание произведения двух некоррелированных случайных величин равно произведению их математических ожиданий.
4- Дисперсия произведения независимых случайных величин:
Доказательство.
Задача 7.3.
Экзаменационный Билет №18 Нормальное распределение случайных величин, его характеристики. Найдем функцию распределения F(x) случайной величины X, распределенной по нормальному закону с параметрами m, σ. Плотность распределения величины X равна:
Математическое ожидание: mx=m, а дисперсия Dx=σ2.  Отсюда находим функцию распределения: Мерой точности называется величина, обратно пропорциональная среднему квадратическому отклонению σ: Пользуясь мерой точности h, можно записать нормальный закон в виде:
2.Теоремы о числовых характеристиках: Математическое ожидание неслучайной величины Если с — неслучайная величина, то 2- Если с — неслучайная величина, то 3- Если с — неслучайная величина, а X — случайная, то т. е. неслучайную величину можно выносить за знак мате матического ожидания. Доказательство. а) Для прерывных величин б) Для непрерывных величин 4- Если с — неслучайная величина, а X — случайная, то т. е. неслучайную величину можно выносить за знак дисперсии, возводя ее в квадрат. Доказательство. По определению дисперсии
Следствие 5- математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий.
Доказательство.
Задача 7.8.
Экзаменационный Билет №19 |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 181. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 имеет показательное (экспоненциальное) распределение с параметром
имеет показательное (экспоненциальное) распределение с параметром 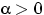 , и пишут:
, и пишут:  , если
, если 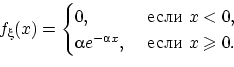

 ,
,  ,
,  ,
,  .
.


 Тогда
Тогда 

 — корреляционный момент величин
— корреляционный момент величин 




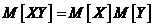





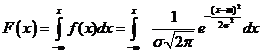




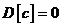
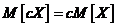


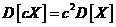

 т. е. неслучайную величину можно выносить за знак среднего квадратического отклонения ее абсолютным значением.
т. е. неслучайную величину можно выносить за знак среднего квадратического отклонения ее абсолютным значением.

