
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Свойства плотности распределения. ⇐ ПредыдущаяСтр 10 из 10 Свойство 1. Свойство 2.Плотность распределения—неотрицательная функция: Свойство 3.Несобственный интеграл от плотности распределения в пределах от -∞ до +∞ равен единице: Свойство 4.Вероятность того, что непрерывная случайная величина Х примет значение из множества В, равна интегралу по множеству В от плотности распределения.
Свойство 2.Для того чтобы Свойство 3.Если случайные величины независимы, то они некоррелированы, т.е. r=0. Док-во: Пусть Х и Y—независимы, тогда по свойству математического ожидания Опр.Две случайные величины Х и Y называют коррелированными, если их коэффициент корреляции отличен от нуля. Опр. Случайные величины Х и Y называют некоррелированнымиесли их коэффициент корреляции равен 0. Замечание. Из коррелированности двух случайных величин следует их зависимость, но из зависимости еще не вытекает коррелированность. Из независимости двух случайных величин следует их некоррелированность, но из некоррелированности еще нельзя заключить о независимости этих величин. Коэффициент корреляции характеризует тенденцию случайных величин к линейной зависимости. Чем больше по абсолютной величине коэффициент корреляции, тем больше тенденция к линейной зависимости. Опр.Коэффициентом асимметрии случайной величины Х называется число Знак коэффициента асимметрии указывает на правостороннюю или левостороннюю асимметрию. 
Характеризует сглаженность кривой распределения по отношению к кривой нормального распределения.
Перейдем к пределу при
Полиномиальное распределение. Предположим, что в результате испытания возможны k исходов E1, E2, …, Ek, P(Ei)=pi,
Свойство 2. Для любых Замечание. Если функция распределения F(x) непрерывная, то свойство выполняется и при замене знаков ≤ и < на < и ≤. Свойство 3. Свойство 4. Функция F(x) непрерывна слева. (т.е. Свойство 5. Вероятность того, что значение случайной величины Х больше некоторого числа х, вычисляется по формуле. Достоверное событие {-∞<x<+∞} представим в виде двух несовместимых событий. Поскольку вероятность достоверного события равна единице, то
|
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 313. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
. . Поскольку F(x)—неубывающая функция, то F’(x)≥0. Следовательно
. Поскольку F(x)—неубывающая функция, то F’(x)≥0. Следовательно  —неотрицательная функция.
—неотрицательная функция. . В формуле (1) подставим х=+∞,
. В формуле (1) подставим х=+∞,  . Поскольку
. Поскольку  , то
, то  .
. .
. необходимо и достаточно, чтобы случайные величины Х и Y были связанны линейной зависимостью. Т.е.
необходимо и достаточно, чтобы случайные величины Х и Y были связанны линейной зависимостью. Т.е.  с вероятностью 1.
с вероятностью 1.


 Опр.Эксцессом случайной величины Х называется число
Опр.Эксцессом случайной величины Х называется число 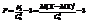 .
.
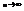 , т.е.
, т.е. 
 .▲
.▲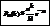 —формула Пуассона.
—формула Пуассона.
 . Тогда вероятность того, что в n независимых испытаниях событие E1 появиться r1 раз, E2 – r2 раз, …, Ek – rk раз вычисляется по формуле:
. Тогда вероятность того, что в n независимых испытаниях событие E1 появиться r1 раз, E2 – r2 раз, …, Ek – rk раз вычисляется по формуле: где
где 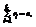
 Эта формула полиномиальное распределения, обобщающая формулу Бернулли.
Эта формула полиномиальное распределения, обобщающая формулу Бернулли.

 ,
,  .
.  ,
, 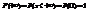 .
. ).
). .
. . Найдем их вероятности
. Найдем их вероятности  .
. . Отсюда
. Отсюда  .
.