
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Свойства плотности распределения случайного вектора.1. 2.
Теорема 1. Пусть 3.
Теорема Пуассона. Теорема. Если вероятность р появления события А в каждом испытании при неограниченном возрастании числа испытаний n изменяется таким образом, что некоторое событие А появится ровно k раз в n независимых испытаниях стремится к величине ▲По формуле Бернулли вероятность того, что событие появится ровно k раз в n независимых испытаниях
Схема независимых испытаний Бернулли. Полиномиальное распределение. Предположим, что в результате испытания возможны два исхода: «У» и «Н», которые мы называем успехом и неудачей. Опр. Последовательность n испытаний называется испытаниями Бернулли, если эти испытания независимы, а в каждом из них возможны два исхода, причем вероятности этих исходов не меняются от испытания к испытанию. Элементарным исходом будет являться: (w1,w2,…,wn),
Таким образом, получим
Случайные величины. Функции распределения и их свойства. Опр. Случайной величиной Хназывается функция X(w), отображающая пространство элементарных исходов Ω во множестве действительных чисел R. Множество значений случайной величины обозначается Ωх.  Опр. Функцией распределения случайной величины Хназывается функция F(x) действительной переменной х, определяющая вероятность того, что случайная величина Х примет в результате эксперимента значение, меньшее некоторого фиксированного числа х. Свойство 1. Функция распределения F(x)–неубывающая функция, т.е. для |
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 330. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

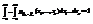 .
. .
. —непрерывный случайный вектор. Тогда случайные величины
—непрерывный случайный вектор. Тогда случайные величины  и
и  — непрерывны, причем
— непрерывны, причем  ,
,  .
. , где
, где  —множество из пространства
—множество из пространства  .
. , то есть
, то есть  .
.


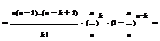

 ,
,  , p+q=1. Предположим, что мы производим независимо друг от друга n таких испытаний.
, p+q=1. Предположим, что мы производим независимо друг от друга n таких испытаний. . Всего таких исходов 2n.
. Всего таких исходов 2n.  . (1)Формула (1) показывает, что события независимы. Обозначим через µ число успехов в n испытаниях Бернулли.
. (1)Формула (1) показывает, что события независимы. Обозначим через µ число успехов в n испытаниях Бернулли.  — вероятность того, что в n испытаниях произошло k успехов. Рассмотрим событие
— вероятность того, что в n испытаниях произошло k успехов. Рассмотрим событие 
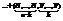 . По теореме сложения получим
. По теореме сложения получим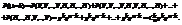
 —формула Бернулли.
—формула Бернулли. .
.  .
. таких что x1<x2
таких что x1<x2  .Пусть х1 и х2 принадлежат множеству Ωх и х1<х2.Событие, состоящее в том, что Х примет значение, меньшее, чем х2, т.е.
.Пусть х1 и х2 принадлежат множеству Ωх и х1<х2.Событие, состоящее в том, что Х примет значение, меньшее, чем х2, т.е.  , представим в виде объединения двух несовместимых событий
, представим в виде объединения двух несовместимых событий 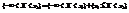 . Тогда по теореме сложения вероятностей получим
. Тогда по теореме сложения вероятностей получим  , т.е.
, т.е.  . Поскольку
. Поскольку  , то
, то 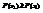 .
.