
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Центральная предельная теорема.Теорема. (Ц.П.Т.).Пусть Х1,Х2,…—последовательность независимых случайных величин, имеющих один и тот же закон распределения и конечное математическое ожидание а и дисперсию G2. Тогда при Замечание 1. Центральная предельная теорема обосновывает тот факт, что нормальное распределение встречается в природе чаще других. Док-во: Свойство 5. Док-во:
Следовательно, Свойство 6.Если Х1,Х2,…,Хn—независимые целочисленные случайные величины, то производящая функция Док-во:
Свойство 2.Характеристическая функция случайной величины Док-во: Свойство 3.Если случайные величины Свойство 4.Если М
Отсюда |
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 335. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
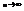 вероятность того, что
вероятность того, что 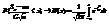 , где
, где  . N(x)—функция стандартного нормального распределения.
. N(x)—функция стандартного нормального распределения.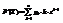 .
.  .
.
 . Если Z=1
. Если Z=1  .
. .
. .
. .
.
 .
. , где a, b—некоторые числа.
, где a, b—некоторые числа.  .
.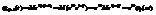 .
. —независимы, то характеристическая функция суммы данных случайных величин равна произведению характеристических функций этих случайных величин, т.е.
—независимы, то характеристическая функция суммы данных случайных величин равна произведению характеристических функций этих случайных величин, т.е. 
 .
. , характеристическая функция случайной величины
, характеристическая функция случайной величины  n раз дифференцируема, причем
n раз дифференцируема, причем  , где
, где  .
. (т.к.
(т.к.  ).
).