
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дискретные случайные величины. Законы распределения биномиальное, геометрическое и Пуассона.Опр. Случайная величина Х называется дискретной, если она принимает конечное либо счетное число значений, т.е. Ωх—конечно или счетно. Опр. Законом распределения дискретной случайной величины Х называется совокупность пар чисел вида (хi, рi), где xi—возможные значения случайной величины, а pi—вероятности, с которыми случайная величина принимает эти значения, т.е. Опр. Говорят, что дискретная случайная величина Х имеет биномиальное распределение с параметрами (n,p), если она может принимать целые неотрицательные значения Опр. Говорят, что случайная величина Х имеет распределение Пуассона с параметром λ (λ>0), если она принимает целые неотрицательные значения Опр. Говорят, что случайная величина Х имеет геометрическое распределение с параметром р (0<р<1), если она принимает натуральные значения
Мат ожидание ДСВ и их свойства. Опр. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности. Обозначают математическое ожидание случайной величины Х через MX или М(Х). Свойства математического ожидания: Свойство 1. Математическое ожидание постоянной величины равно самой постоянной: M(C)=C.Будем рассматривать постоянную С как дискретную случайную величину, которая принимает одно возможное значение С с вероятностью 1. Следовательно,  Свойство 2. Постоянный множитель можно выносить за знак математического ожидания: M(CX)=CM(X). Ряд распределения случайной величины СХ
Математическое ожидание случайной величины СХ Опр.Случайные величины X1,X2,…,Xn называются независимыми, если для любых числовых множеств B1,B2,…,Bn
Дисперсия, свойства. Начальные и центральные моменты. Опр. Дисперсией случайной величины называется число Опр. Средним квадратическим отклонением случайной величины Х называется число
Свойства дисперсии. Свойство 1.Дисперсия постоянной величины С равна 0.DC=0.
Свойство 2.Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
Свойство 3.Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:
Непрерывные случайные величины. Свойства плотности распределения. Опр. Говорят, что случайная величина Х имеет плотность вероятности или плотность распределения вероятностей Опр.Случайная величина называется непрерывной, если она имеет плотность распределения. Пусть р(х)—непрерывная функция. Тогда
|
||||||||||||||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 360. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , причем
, причем 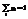 .
.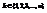 с вероятностями
с вероятностями  .
. 
 с вероятностями
с вероятностями 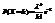 . Обозначают
. Обозначают 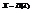 , т.е. случайная величина Х имеет распределение Пуассона с параметром λ.
, т.е. случайная величина Х имеет распределение Пуассона с параметром λ. 
 с вероятностями
с вероятностями  , где q=1-p.
, где q=1-p. .
. – случайная величина Х принимает конечное число значений.
– случайная величина Х принимает конечное число значений. 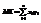 – принимает счетное число значений, причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
– принимает счетное число значений, причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно. .
. .
.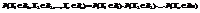 .
.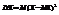 .
. .
.
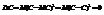 .
. .
. .
. .
.
 , если существует функция p(x) такая, что функция распределения
, если существует функция p(x) такая, что функция распределения  (1).
(1). Где
Где  , α—бесконечно малая величина при Δх→0. Т.к.
, α—бесконечно малая величина при Δх→0. Т.к.  , при Δх→0. Таким образом,
, при Δх→0. Таким образом,  .
. 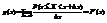 .
.