
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
События и операции над ними. Относительные частоты и их свойстваПервичным понятием ТВ, неопределяемым через другие понятия, является пространство элементарных исходов Ω. Обычно в качестве пространства элементарных исходов берутся единственно возможные неразложимые результаты эксперимента. Опр. Событиемназ. произвольное подмножество А пространства элементарных исходов Ω, т.е. элементарные исходы, из которых состоит событие А, называются благоприятствующими событию А. Говорят, что событие А произошло, если в результате эксперимента наступает элементарный исход w
Аксиомы теории вероятностей. Дискретные пространства элементарных исходов. Классическое определение вероятности. Пусть Ω—пространство элементарных исходов. Предположим, что F—множество всех подмножеств Ω. Опр. Событие—это подмножество Ω, принадлежащее классу F. Любому событию ставится в соответствие действительное число, называемое вероятностью этого события, т.е.  Элементы комбинаторики. Основные правила. Лемма 1. Из m элементов а1,…,аm первой группы и n элементов b1,…,bn второй группы можно составить ровно m∙n упорядоченных пар вида (аi, bj), содержащих по одному элементу из каждой группы. Лемма 2. Из n1 элементов первой группы a1, а2,…, аn1, n2 элементов второй группы b1, b2,…, bn2, и т.д. nk элементов k-ой группы x1, x2,…, xnk можно составить ровно n1∙ n2∙…∙nk различных упорядоченных комбинаций вида |
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 370. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 A, т.е. благоприятствующий событию А. Опр. Все пространство элементарных исходов Ω, если его взять в качестве события, наз. достоверным событием, т.е. оно происходит в любом эксперименте (всегда). Опр. Пустое множество
A, т.е. благоприятствующий событию А. Опр. Все пространство элементарных исходов Ω, если его взять в качестве события, наз. достоверным событием, т.е. оно происходит в любом эксперименте (всегда). Опр. Пустое множество  (т.е. множество, кот. не содержит ни одного элементарного исхода) наз. невозможным событием, т.к. оно никогда не происходит. Опр. Все остальные события, кроме Ω и
(т.е. множество, кот. не содержит ни одного элементарного исхода) наз. невозможным событием, т.к. оно никогда не происходит. Опр. Все остальные события, кроме Ω и  , т.е. событие
, т.е. событие  , когда происходит хотя бы одно из событий А или В. Опр. Произведением событий А и В наз. пересечение множеств
, когда происходит хотя бы одно из событий А или В. Опр. Произведением событий А и В наз. пересечение множеств 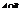 (А
(А  В), т.е. событие АВ порисходит, когда А и В происходят одновременно. Опр. Разностью событий А и В наз. разность множеств А\В. Событие А\В происходит <=>, когда происходит А и не происходит В.
В), т.е. событие АВ порисходит, когда А и В происходят одновременно. Опр. Разностью событий А и В наз. разность множеств А\В. Событие А\В происходит <=>, когда происходит А и не происходит В.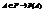 так, что при этом выполняются аксиомы ТВ. Аксиома 1 Вероятность любого события неотрицательна
так, что при этом выполняются аксиомы ТВ. Аксиома 1 Вероятность любого события неотрицательна 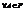
 . Аксиома 2 Вероятность достоверного события равна 1, т.е.
. Аксиома 2 Вероятность достоверного события равна 1, т.е. 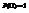 Аксиома 3(счетной аддитивности). Если события
Аксиома 3(счетной аддитивности). Если события 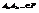 и
и  при
при  , то вероятность их суммы равна сумме вероятностей. Опр. Бесконечное множество наз. счетным, если элементы этого множества можно занумеровать натуральными числами. Все другие бесконечные множества называются несчетными. Опр. Пространство элементарных исходов наз. дискретным, если оно конечно или счетно, т.е.
, то вероятность их суммы равна сумме вероятностей. Опр. Бесконечное множество наз. счетным, если элементы этого множества можно занумеровать натуральными числами. Все другие бесконечные множества называются несчетными. Опр. Пространство элементарных исходов наз. дискретным, если оно конечно или счетно, т.е.  или
или  . Любому элементарному исходу (
. Любому элементарному исходу (  )ставится в соответствие число
)ставится в соответствие число  так, что при этом
так, что при этом  .
. , содержащих по одному элементу из каждой группы. Леммы 1 и 2 наз. основными правилами комбинаторики.
, содержащих по одному элементу из каждой группы. Леммы 1 и 2 наз. основными правилами комбинаторики.