
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема 3. (Закон больших чисел в форме Бернулли).Пусть μ—число успехов в n независимых испытаниях Бернулли с вероятностью успеха р в одном испытании, тогда Док-во: Введем случайные величины μi—число успехов в i-ом испытании. Тогда
В чем смысл закона больших чисел в форме Бернулли? Пусть в результате эксперимента может произойти или не произойти событие А. P(A)—вероятность события А в одном эксперименте. Эксперимент повторяется N раз, N(A)—число появлений события А в этих N экспериментах. Таким образом, закон больших чисел в форме Бернулли теоретически подтверждает устойчивость относительных частот, т.е. стабилизацию при большом числе испытаний относительной частоты вокруг вероятности (относительная частота ≈Р(А)).
Замечание 2. При больших
Если взять B1=]-∞,x1[ ; B2=]-∞,x2[ ; … ; Bn=]-∞,xn[, то
Свойство 3.Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: Свойство 4.Математическое ожидание суммы двух случайных величин рано сумме математических ожиданий слагаемых: Теорема 1. Математическое ожидание числа появлений события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании: Будем рассматривать в качестве случайной величины Х число появлений события А в n независимых испытаниях. Очевидно, общее число Х появлений события А в этих испытаниях складывается из чисел появлений события в отдельных испытаниях. Поэтому если Х1—число появлений события в первом испытании, Х2—во втором,…, Хn—в n-ом, то общее число появлений события 
Теорема 2. Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятность появления и непоявления события в одном испытании: Случайная величина Х—число появлений события А в n независимых испытаниях.
Опр. Начальным моментом порядка kслучайной величиныХназывают математическое ожидание случайной величины Хk: Опр. Центральным моментом порядка kслучайной величины Х называют математическое ожидание величины (Х-МХ)k.
|
||||||||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 328. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
.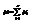 .
.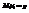 ,
,  (т.к.
(т.к. 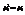 ).
).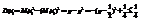 (т.е. дисперсия ограничена
(т.е. дисперсия ограничена 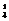 ). μ1, μ2,…, μn—независимы. По закону больших чисел в форме Чебышёва
). μ1, μ2,…, μn—независимы. По закону больших чисел в форме Чебышёва 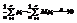 .
.  .
.  —относительная частота появления события А.
—относительная частота появления события А.  . N(A)=μ,
. N(A)=μ, 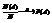 .
.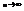
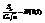 , поэтому
, поэтому  . ЦПТ можно записать в другой форме:
. ЦПТ можно записать в другой форме:  .
.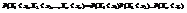 .
.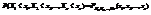 —совместимая функция распределения случайных величин Х1,Х2,…,Хn. Таким образом,
—совместимая функция распределения случайных величин Х1,Х2,…,Хn. Таким образом,  .
. .
. .
.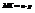 .
. . По свойству 4:
. По свойству 4: . А
. А 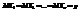 . Таким образом, получим
. Таким образом, получим  .
. .
. . Т.к. MX1=p.
. Т.к. MX1=p. 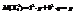 , то
, то  . Очевидно, что дисперсия остальных случайных величин также равна pq, откуда
. Очевидно, что дисперсия остальных случайных величин также равна pq, откуда  . В частности,
. В частности,  ,
,  .
.  —>
—>  .
. . В частности
. В частности 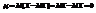 ,
, 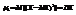 —>
—>  .
.