
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Функция двух случайных аргументов. Формула свертки.Стр 1 из 10Следующая ⇒ Равномерное, показательное, нормальное распределения. Их функции распределения. Опр. Говорят, что случайная величина Х равномерно распределена на отрезке [a, b], если она непрерывна и имеет плотность вероятности: Найдем функцию распределения равномерно распределенной случайной величины X. а) x≤a б) a<x≤b в) x>b
Лемма о нормальном распределении. Критерий независимости дискретной и непрерывной СВ. Теорема 1. Если случайная величина Х имеет нормальное стандартное распределение с параметрами (a, Теорема 2. (Критерий независимости дискретных случайных величин). Для того чтобы дискретные случайные величины Х1,…,Хn были независимы, необходимо и достаточно, чтобы для любых действительных чисел х1,…,хn выполнялось соотношение Теорема 3. (Критерий независимости для непрерывных случайных величин). Для того чтобы непрерывные случайные величины Х1, Х2,…,Хn были независимыми, необходимо и достаточно, чтобы для любых действительных чисел х1,…,хn выполнялось соотношение
Случайный вектор. Свойства функций распределения случайного вектора. Опр. Вектор Т.о., случайный вектор Опр. Функция
 Свойства функции распределения случайного вектора: Свойство 1. Свойство 2. Функция распределения случайного вектора неубывающая по каждому аргументу. ▲ Пусть x1<y1, тогда событие
Случайный вектор. Свойства плотности распределения Опр. Вектор Т.о., случайный вектор Опр. Функция
Опр. Случайный вектор называется дискретным, если все его компоненты—дискретные случайные величины. Опр. Случайный вектор
Функция двух случайных аргументов. Формула свертки. Опр. Если каждой паре возможных значений случайных величин X и Y соответствует одно возможное значение случайной величины Z, то Z называют функцией двух случайных аргументов X и Y: Случай 1.Пусть Х и Y—дискретные независимые случайные величины. Для того чтобы составить закон распределения функции Z=X+Y, надо найти все возможные значения Z и их вероятности. Иными словами, составляется ряд распределения случайной величины Z. Рассмотрим общий случай: Пусть Х и Y—независимые случайные величины, принимающие значения
|
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 324. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
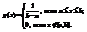
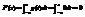 ;
; .
.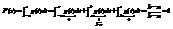 .
.


 ), то случайная величина
), то случайная величина  имеет нормальное распределение, т.е.
имеет нормальное распределение, т.е. 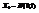 . ▲
. ▲  ;
;  .▲
.▲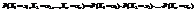 .
. . Где
. Где 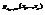 совместимая плотность распределения случайных величин Х1,…,Хn, то есть совместимая функция распределения случайных величин Х1,…,Хn
совместимая плотность распределения случайных величин Х1,…,Хn, то есть совместимая функция распределения случайных величин Х1,…,Хn .
. , где
, где  —случайные величины, называются n-мерным случайным вектором.
—случайные величины, называются n-мерным случайным вектором. отображает пространство элементарных исходов Ω→
отображает пространство элементарных исходов Ω→  в n-мерное действительное пространство
в n-мерное действительное пространство 
 называется функцией распределения случайного вектора
называется функцией распределения случайного вектора  .
. .
. . Тогда
. Тогда  . По свойству вероятности если
. По свойству вероятности если  , то
, то  , получим
, получим  . Т.е. функция не убывает по первому аргументу. Аналогично для любого аргумента. ▲
. Т.е. функция не убывает по первому аргументу. Аналогично для любого аргумента. ▲ называется непрерывным, если существует неотрицательная функция
называется непрерывным, если существует неотрицательная функция  , называется плотностью распределения случайных величин
, называется плотностью распределения случайных величин 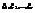 такая, что функция распределения
такая, что функция распределения 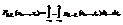 .
.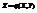 .
.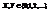 . Обозначим через
. Обозначим через 
 ,
, 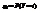 ,
,  . Z=X+Н. Обозначим через
. Z=X+Н. Обозначим через 


 . Таким образом,
. Таким образом,  —формула свертки.
—формула свертки.