
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Число выборок, свойства сочетаний, геометрические вероятности.Общая таблица числа выбора:
Опр. Упорядоченная выборка без возвращения наз. размещением. Число размещений Свойства вероятности. 1)Вероятность невозможного события равна 0, т.е. 2)Вероятность достоверного события равна 1, т.е. .3) Для любого события вероятность лежит в пределах от 0 до 1, т.е. 4)(Теорема сложения вероятностей): если события А и В несовместимы, то вероятность их суммы равна сумме вероятностей этих событий, т.е. Р(А+В)=Р(А)+Р(В). Док-во: 5)(обобщенная теорема сложения вероятностей)
Условная вероятность.Независимость. Опр. Условной вероятностьюсобытия B при условии A называется вероятность события B в предположении, что событие A наступило. Обозначение Теорема (умножение вероятностей): Теорема (обобщенная теорема умножения). Доказательство:
Опр. События А и В называются независимыми, если Свойство. События А и В независимы тогда и только тогда когда P(B/A)=P(B). Опр. События А1,А2,…,Аn называются независимыми (или независимыми в совокупности), если 
Формула полной вероятности и Байеса. Теорема 1.Если события Н1, Н2,…,Нn образуют полную группу, то вероятность любого события А можно вычислить по формуле полной вероятности: Теорема 2.Пусть события Н1, Н2, …, Нn образуют полную группу, А–некоторое событие, причем P(A)≠0, тогда имеет место формула Байеса:
Доказательство: По теореме умножения вероятностей
Локальная и интегральная теоремы Муавра-Лапласа. Теорема (локальная теорема Муавра-Лапласа). Если вероятность появления события А в каждом отдельном испытании постоянная и отлична от 0 и 1, т.е. 0<p<1, то вероятность того, что событие А появится ровно k раз в n независимых испытаниях.
Имеются специальные таблицы значений функций φ(х). Нужно учитывать, что функция φ(х)–четная, т.е. φ(х)=φ(-х). |
|||||||||||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 333. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |



 . Опр. Перестановкой из k элементов наз. совокупность этих же элементов, записанных в произвольном порядке. Pk-число перестановок из k элементов:
. Опр. Перестановкой из k элементов наз. совокупность этих же элементов, записанных в произвольном порядке. Pk-число перестановок из k элементов:  . Опр. Произвольное k-элементное подмножество множества из n элементов наз. сочетанием из n элементов по k элементов. Сочетание—это неупорядоченная выборка объема k из n элементов. Обозначается число всех сочетаний из n элементов по k элементов через
. Опр. Произвольное k-элементное подмножество множества из n элементов наз. сочетанием из n элементов по k элементов. Сочетание—это неупорядоченная выборка объема k из n элементов. Обозначается число всех сочетаний из n элементов по k элементов через  :
:  , 0≤k≤n. Свойства сочетаний: 1)
, 0≤k≤n. Свойства сочетаний: 1)  ; 2)
; 2)  . Док-во :
. Док-во :  3)
3)  4)
4)  Док-во:
Док-во:  .
.  . Док-во:
. Док-во:  .
. . Док-во:
. Док-во: 
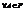
 . Д-во:
. Д-во: 
 ;
; 
 .Док-во:
.Док-во: 

 , (реже
, (реже  ).
).  .
.  .
. .
. .
.

 .
. .
. . Пусть P(B/A)=P(B), тогда
. Пусть P(B/A)=P(B), тогда 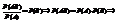 А и В независимы.
А и В независимы. (для i≠j; i,j
(для i≠j; i,j  {1,2,3,…,n})–попарная независимость событий;
{1,2,3,…,n})–попарная независимость событий;  , …,
, …, .
.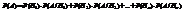 , или
, или  . ▲Так как события образуют полную группу, то можно записать
. ▲Так как события образуют полную группу, то можно записать  . Событие А может произойти только с одним из событий Hi, i
. Событие А может произойти только с одним из событий Hi, i 
 ▲
▲ ,
, 
 . Отсюда находим вероятность
. Отсюда находим вероятность  . Остается в знаменателе подставить вместо
. Остается в знаменателе подставить вместо  —формула полной вероятности.
—формула полной вероятности. , где
, где  ;
;  , q=1-p.
, q=1-p.