
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Числовые характеристики системы дискретных СВ (математическое ожидание, дисперсия, ковариация, коэффициент линейной корреляции и его свойства).(тетр) ⇐ ПредыдущаяСтр 10 из 10 Математическим ожиданием М(Х) дискретной случайной величины Х называется сумма произведений всех ее возможных значений
Математическое ожидание называют также средним значением случайной величины Х, подчеркивая статистический смысл понятия, или центром распределения случайной величины Х (по аналогии с понятием центра тяжести для системы материальных точек). Свойства математического ожидания: 1) если случайная величина Х принимает постоянное значение Х=С= =const, то М(С)=С; 2) М(СХ)=СМ(Х), С = const; 3) Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий: M(X+Y)=M(X)+M(Y); 4) Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий: M(X×Y)=M(X)×M(Y). Наряду с характеристиками положения большую роль играют характеристики рассеяния. Рассеяние случайной величины Х связано с отклонением этой величины от ее центра распределения М(Х). Чтобы учитывать отклонения противоположных знаков, удобно рассматривать квадраты отклонений. Дисперсией D(X) случайной величины Х называют средний квадрат отклонения случайной величины от ее центра распределения:
Используя свойства математического ожидания, можно записать более удобную формулу для подсчета дисперсии
Для того, чтобы рассматривать отклонение в тех же единицах, что и значения случайной величины, вводится еще одна характеристика – среднее квадратическое отклонение s(Х), которое определяется как
Свойства дисперсии: 1) D(X) ³ 0; 2) если С=const, то D(С) = 0; 3) 4) D(X ± Y) = D(X) + D(Y).  Корреляционным моментом или ковариацией случайных величин Х и У называется математическое ожидание произведения соответствующих центрированных величин Если случайные величины независимы, то их ковариация равна нулю. Обратное утверждение верно не всегда. Равенство нулю ковариации независимых случайных величин следует из теоремы о математическом ожидании произведения независимых случайных величин часто силу зависимости между случайными величинами характеризуют безразмерным коэффициентом
[1] Математическое ожидание называют еще средним значением, а также центром распределения. [2] Для математического ожидания употребляются и другие обозначения: [3] Две случайные величины являются независимыми, если закон распределения одной из них не зависит от того, какие значения приняла другая случайная величина. [4] Дисперсию обозначают еще [5] Ляпунов Александр Михайлович (1857–1918) ― русский математик и механик. [6] Гаусс Карл Фридрих (Gauss C. F., 1777–1855) ― немецкий математик. |
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 296. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 на соответствующие вероятности
на соответствующие вероятности 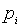 :
:
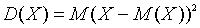
 .
.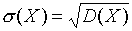 .
. , С=const;
, С=const;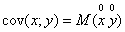


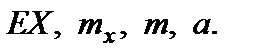
 (читается “сигма квадрат”).
(читается “сигма квадрат”).