
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Вероятность попадания значений нормальной СВ в интервал, симметричный относительно математического ожидания, правило трех сигм.Вероятность Если в этом равенстве положить s w:space="720"/></w:sectPr></w:body></w:wordDocument>"> То есть нормально распределенная СВ X отклоняется от своего М.О. a, как правило, менее чем на 3 Функция одной случайной величины. Математическое ожидание функции одной СВ.(тетр) Если каждому возможному значению случайной величины Хсоответствует одно возможное значение случайной величины Y, то Y называют функцией случайного аргу-мента Х: Y = φ(X). Выясним, как найти закон распределения функции по известному закону распределения аргумента. 1) Пусть аргумент Х – дискретная случайная величина, причем различным значениям Хсоот-ветствуют различные значения Y. Тогда вероятности соответствующих значений Х и Yравны. 2) Если разным значениям Х могут соответствовать одинаковые значения Y, то вероятности значений аргумента, при которых функция принимает одно и то же значение, складываются. 3) Если Х – непрерывная случайная величина, Y = φ(X), φ(x) – монотонная и дифференцируемая функция, а ψ(у) – функция, обратная к φ(х). |
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 307. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
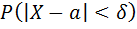 того, что отклонение СВ X от её М.О. a по абсолютной величине будет меньше заданного положительного числа
того, что отклонение СВ X от её М.О. a по абсолютной величине будет меньше заданного положительного числа 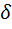 , равна
, равна 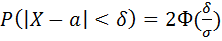
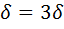 ,то получим
,то получим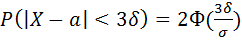 ,
,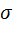 .В этом и состоит так называемое правило 3 сигм, которым часто пользуются в математической статистике.
.В этом и состоит так называемое правило 3 сигм, которым часто пользуются в математической статистике.