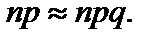Биномиальное распределение и распределение Пуассона.

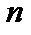Биномиальное распределение.К этому распределению приводит схема Бернулли. Пусть производится  независимых повторных испытаний, в каждом из которых вероятность появления события  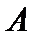постоянна и равна  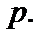Тогда случайная величина  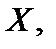означающая число появления события  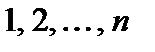в  испытаниях, может принимать значения  с вероятностями, вычисляемыми по формуле Бернулли: 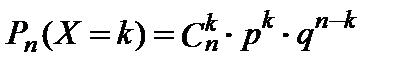, где 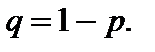 Такое распределение дискретной случайной величины  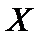называют биномиальным. Параметрами биномиального распределения являются 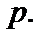и  Кратко биномиальное распределение с параметрами 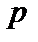и записывают в виде 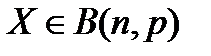. Математическое ожидание и дисперсия биномиальной случайной величины  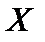соответственно равны: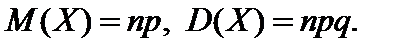

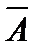Распределение Пуассона. Если в биномиальном распределении вероятность события  (или ) в одном испытании равна  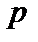(или 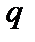) и очень мала, но число испытаний  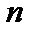достаточно велико, причем произведение  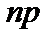сохраняет постоянное значение (то есть среднее число появления события  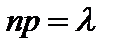в различных сериях испытаний  остается неизменным), а именно , то случайная величина  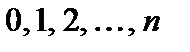— число появлений события  в  опытах — может принимать значения  с вероятностями, вычисляемыми по формуле Пуассона: 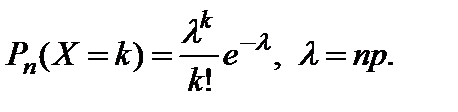Такое распределение дискретной случайной величины  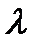называется распределением Пуассона. Параметром распределения Пуассона является постоянная величина , которой равны как математическое ожидание так и дисперсия, то есть  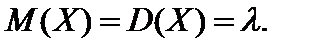Поэтому распределение Пуассона может служить оценкой точного биноминального распределения дискретной случайной величины, если ее математическое ожидание мало отличается от дисперсии, то есть