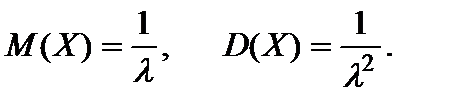Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Равномерное распределение, показательный закон распределения.Равномерное распределение.Непрерывная случайная величина
Графики функций Математическое ожидание и дисперсия случайной величины
К показательному распределению приводят задачи о длительности безаварийной работы различных машин и приборов. Оно играет особую роль в теории массового обслуживания и надежности, в страховом деле, демографии и многих других прикладных дисциплинах. |
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 412. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
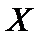 называется равномерно распределенной на отрезке
называется равномерно распределенной на отрезке 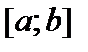 , если плотность вероятностей этой величины постоянна на данном отрезке и равна нулю вне этого отрезка. Плотность вероятностей
, если плотность вероятностей этой величины постоянна на данном отрезке и равна нулю вне этого отрезка. Плотность вероятностей  и функция распределения
и функция распределения  равномерно распределенной на отрезке
равномерно распределенной на отрезке 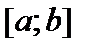 случайной величины
случайной величины 


 Равномерное распределение имеет важное практическое значение, ибо многие случайные величины, представляющие интерес, распределены по этому закону и с его помощью можно получить практически любое распределение. Показательный закон распределения. Если плотность распределения непрерывной случайной величины
Равномерное распределение имеет важное практическое значение, ибо многие случайные величины, представляющие интерес, распределены по этому закону и с его помощью можно получить практически любое распределение. Показательный закон распределения. Если плотность распределения непрерывной случайной величины  то говорят, что случайная величина
то говорят, что случайная величина  . Функция распределения
. Функция распределения 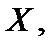 распределенной по показательному закону, имеет вид
распределенной по показательному закону, имеет вид  Графики функций
Графики функций  Математическое ожидание и дисперсия непрерывной случайной величины
Математическое ожидание и дисперсия непрерывной случайной величины  распределенной по показательному закону с параметром
распределенной по показательному закону с параметром  соответственно равны:
соответственно равны: