
Студопедия
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
|
Нормальный закон распределения непрерывной СВ. Вероятность попадания значений нормальной случайной величины в заданный полуинтервал.
Нормальное распределение.Фундаментальное значение в теории вероятностей имеет нормальное распределение. С ним приходится сталкиваться при анализе ошибок различных измерений, отклонений в размерах от типичных у каких-либо объектов, животных, растений и т.д. Широкое распространение нормального распределения объясняет центральная предельная теорема теории вероятностей (теорема Ляпунова[5]). Одна из простейших форм этой теоремы утверждает: если 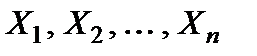 — независимые случайные величины, имеющие один и тот же закон распределения с математическим ожиданием — независимые случайные величины, имеющие один и тот же закон распределения с математическим ожиданием 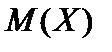 и дисперсией и дисперсией  то при неограниченном увеличении то при неограниченном увеличении 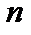 закон распределения суммы закон распределения суммы  неограниченно приближается к нормальному. Главная особенность нормального распределения состоит в том, что он является предельным законом, к которому приближаются другие законы распределения.Говорят, что непрерывная случайная величина неограниченно приближается к нормальному. Главная особенность нормального распределения состоит в том, что он является предельным законом, к которому приближаются другие законы распределения.Говорят, что непрерывная случайная величина 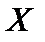 распределена понормальному закону, если ее функция плотности вероятностей имеет вид: распределена понормальному закону, если ее функция плотности вероятностей имеет вид: 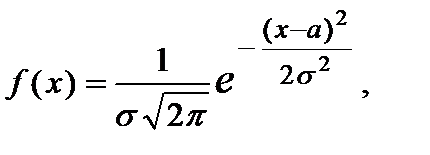 (20) где а и (20) где а и  — параметры распределения, причем — параметры распределения, причем 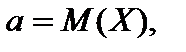  График функции (20) называют кривой нормального распределения или кривой Гаусса[6].Исследование функции (20) показывает, что эта функция определена и положительна на всей числовой прямой. Функция График функции (20) называют кривой нормального распределения или кривой Гаусса[6].Исследование функции (20) показывает, что эта функция определена и положительна на всей числовой прямой. Функция 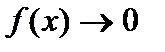 при при  то есть ось то есть ось 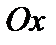 является горизонтальной асимптотой. Функция является горизонтальной асимптотой. Функция  в точке в точке 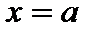 достигает максимума, равного достигает максимума, равного  Кривая нормального распределения симметрична относительно прямой Кривая нормального распределения симметрична относительно прямой 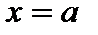 и имеет перегиб в точках, абсциссы которых равны и имеет перегиб в точках, абсциссы которых равны 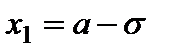 и и  а ординаты — а ординаты —  При изменении параметра При изменении параметра 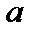 и постоянном и постоянном  форма кривой не меняется, при этом кривая перемещается вдоль оси форма кривой не меняется, при этом кривая перемещается вдоль оси 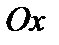 (с увеличением параметра (с увеличением параметра  график сдвигается вправо, а при умень уменьшении график сдвигается вправо, а при умень уменьшении 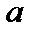 — влево: рис. 11а), а при изменении параметра — влево: рис. 11а), а при изменении параметра  меняется форма нормальной кривой (с уменьшением меняется форма нормальной кривой (с уменьшением  кривая становиться все более островершинной: рис. 11б).Площадь, заключенная под кривой нормального распределения, всегда равна единице.Функция распределения случайной величины кривая становиться все более островершинной: рис. 11б).Площадь, заключенная под кривой нормального распределения, всегда равна единице.Функция распределения случайной величины 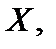 распределенной по нормальному закону, имеет вид распределенной по нормальному закону, имеет вид  Последний интеграл нельзя вычислить по формуле Ньютона-Лейбница. Однако функцию Последний интеграл нельзя вычислить по формуле Ньютона-Лейбница. Однако функцию 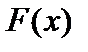 можно выразить через табулированную функцию Лапласа можно выразить через табулированную функцию Лапласа 
если воспользоваться подстановкой  В результате получим: В результате получим: 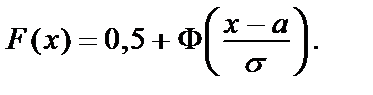 (21)Из равенств (13) и (21) легко получить формулу для нахождения вероятности попадания значений нормальной случайной величины (21)Из равенств (13) и (21) легко получить формулу для нахождения вероятности попадания значений нормальной случайной величины 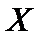 в полуинтервал в полуинтервал 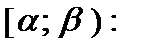 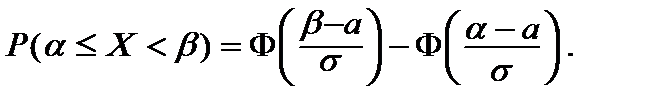 (22) (22)
В частности, вероятность 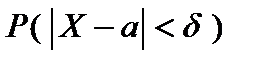 того, что отклонение случайной величины того, что отклонение случайной величины 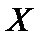 от ее математического ожидания а по абсолютной величине будет меньше заданного положительного числа от ее математического ожидания а по абсолютной величине будет меньше заданного положительного числа  , равна , равна  (23)Если в равенстве (23) положить (23)Если в равенстве (23) положить  , то получим , то получим 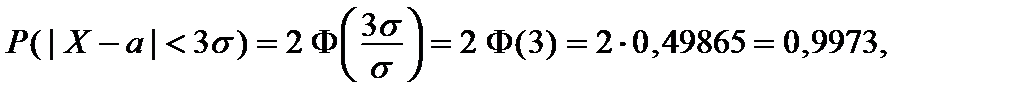 то есть нормально распределенная случайная величина то есть нормально распределенная случайная величина 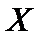 отклоняется от своего математического ожидания отклоняется от своего математического ожидания  как правило, менее чем на как правило, менее чем на 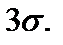 В этом и состоит так называемое правило трех сигм, которым часто пользуются в математической статистике. В этом и состоит так называемое правило трех сигм, которым часто пользуются в математической статистике.
|


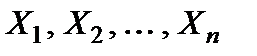 — независимые случайные величины, имеющие один и тот же закон распределения с математическим ожиданием
— независимые случайные величины, имеющие один и тот же закон распределения с математическим ожиданием 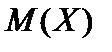 и дисперсией
и дисперсией  то при неограниченном увеличении
то при неограниченном увеличении 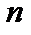 закон распределения суммы
закон распределения суммы  неограниченно приближается к нормальному. Главная особенность нормального распределения состоит в том, что он является предельным законом, к которому приближаются другие законы распределения.Говорят, что непрерывная случайная величина
неограниченно приближается к нормальному. Главная особенность нормального распределения состоит в том, что он является предельным законом, к которому приближаются другие законы распределения.Говорят, что непрерывная случайная величина 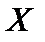 распределена понормальному закону, если ее функция плотности вероятностей имеет вид:
распределена понормальному закону, если ее функция плотности вероятностей имеет вид: 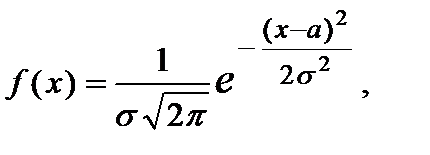 (20) где а и
(20) где а и  — параметры распределения, причем
— параметры распределения, причем 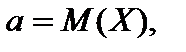
 График функции (20) называют кривой нормального распределения или кривой Гаусса[6].Исследование функции (20) показывает, что эта функция определена и положительна на всей числовой прямой. Функция
График функции (20) называют кривой нормального распределения или кривой Гаусса[6].Исследование функции (20) показывает, что эта функция определена и положительна на всей числовой прямой. Функция 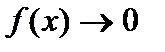 при
при  то есть ось
то есть ось 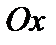 является горизонтальной асимптотой. Функция
является горизонтальной асимптотой. Функция  в точке
в точке 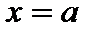 достигает максимума, равного
достигает максимума, равного  Кривая нормального распределения симметрична относительно прямой
Кривая нормального распределения симметрична относительно прямой 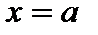 и имеет перегиб в точках, абсциссы которых равны
и имеет перегиб в точках, абсциссы которых равны 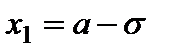 и
и  а ординаты —
а ординаты —  При изменении параметра
При изменении параметра 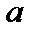 и постоянном
и постоянном  форма кривой не меняется, при этом кривая перемещается вдоль оси
форма кривой не меняется, при этом кривая перемещается вдоль оси 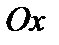 (с увеличением параметра
(с увеличением параметра  график сдвигается вправо, а при умень уменьшении
график сдвигается вправо, а при умень уменьшении 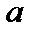 — влево: рис. 11а), а при изменении параметра
— влево: рис. 11а), а при изменении параметра  меняется форма нормальной кривой (с уменьшением
меняется форма нормальной кривой (с уменьшением  кривая становиться все более островершинной: рис. 11б).Площадь, заключенная под кривой нормального распределения, всегда равна единице.Функция распределения случайной величины
кривая становиться все более островершинной: рис. 11б).Площадь, заключенная под кривой нормального распределения, всегда равна единице.Функция распределения случайной величины 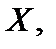 распределенной по нормальному закону, имеет вид
распределенной по нормальному закону, имеет вид  Последний интеграл нельзя вычислить по формуле Ньютона-Лейбница. Однако функцию
Последний интеграл нельзя вычислить по формуле Ньютона-Лейбница. Однако функцию 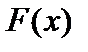 можно выразить через табулированную функцию Лапласа
можно выразить через табулированную функцию Лапласа 
 В результате получим:
В результате получим: 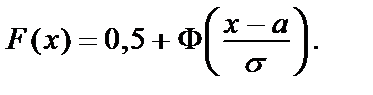 (21)Из равенств (13) и (21) легко получить формулу для нахождения вероятности попадания значений нормальной случайной величины
(21)Из равенств (13) и (21) легко получить формулу для нахождения вероятности попадания значений нормальной случайной величины 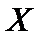 в полуинтервал
в полуинтервал 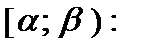
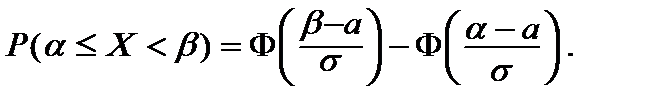 (22)
(22)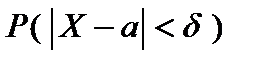 того, что отклонение случайной величины
того, что отклонение случайной величины 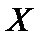 от ее математического ожидания а по абсолютной величине будет меньше заданного положительного числа
от ее математического ожидания а по абсолютной величине будет меньше заданного положительного числа  , равна
, равна  (23)Если в равенстве (23) положить
(23)Если в равенстве (23) положить  , то получим
, то получим 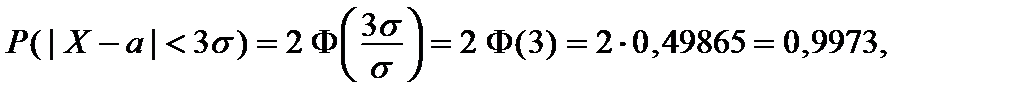 то есть нормально распределенная случайная величина
то есть нормально распределенная случайная величина  как правило, менее чем на
как правило, менее чем на 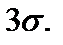 В этом и состоит так называемое правило трех сигм, которым часто пользуются в математической статистике.
В этом и состоит так называемое правило трех сигм, которым часто пользуются в математической статистике.