
Студопедия
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
|
Числовые характеристики случайных величин. Свойства математического ожидания СВ.
Закон распределения полностью характеризует случайную величину с вероятностной точки зрения. Однако при решении многих практических задач знание закона распределения необязательно. Зачастую бывает достаточно указать лишь некоторые характерные черты закона распределения. Для этой цели используют постоянные числа, описывающие случайную величину суммарно — числовые характеристики случайной величины.Важнейшими из них являются математическое ожидание и дисперсия. Математическим ожиданием[1]дискретной случайной величины называют сумму произведений всех ее возможных значений на соответствующие им вероятности. Математическое ожидание случайной величины 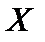 будем обозначать символом[2] будем обозначать символом[2] 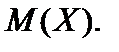 Для дискретной случайной величины Для дискретной случайной величины 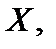 представленной рядом распределения (10), математическое ожидание определяется равенством представленной рядом распределения (10), математическое ожидание определяется равенством  (17). Пусть (17). Пусть 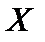 — непрерывная случайная величина, имеющая плотность распределения вероятностей — непрерывная случайная величина, имеющая плотность распределения вероятностей  Тогда математическое ожидание этой случайной величины, возможные значения которой принадлежат отрезку Тогда математическое ожидание этой случайной величины, возможные значения которой принадлежат отрезку 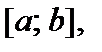 находятся по формуле находятся по формуле  . Если непрерывная случайная величина может принимать любые значения числовой прямой, то . Если непрерывная случайная величина может принимать любые значения числовой прямой, то  . Свойства математического ожидания: 1°. Математическое ожидание постоянной величины равно этой постоянной: . Свойства математического ожидания: 1°. Математическое ожидание постоянной величины равно этой постоянной:  2°.Постоянный множитель можно выносить за знак математического ожидания: 2°.Постоянный множитель можно выносить за знак математического ожидания: 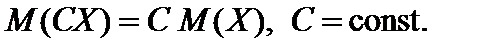 3°.Математическое ожидание алгебраической суммы двух случайных величин 3°.Математическое ожидание алгебраической суммы двух случайных величин 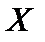 и и 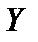 равно алгебраической сумме их математических ожиданий: равно алгебраической сумме их математических ожиданий:  4°. Математическое ожидание произведения двух независимых[3] случайных величин 4°. Математическое ожидание произведения двух независимых[3] случайных величин 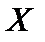 и и 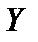 равно произведению их математических ожиданий: равно произведению их математических ожиданий:  Математическое ожидание является числом постоянным, независящим от опыта и характеризующим определенное свойство случайной величины — устойчивость среднего арифметического значений случайной величины, полученных в результате испытаний. Однако этой числовой характеристики не всегда бывает достаточно. Математическое ожидание является числом постоянным, независящим от опыта и характеризующим определенное свойство случайной величины — устойчивость среднего арифметического значений случайной величины, полученных в результате испытаний. Однако этой числовой характеристики не всегда бывает достаточно.
15. Свойства дисперсии СВ. Мода, медиана, начальный и центральный моменты k-го порядка СВ. Коэффициент асимметрии, эксцесс.
Дисперсией[4] 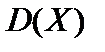 случайной величины случайной величины 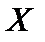 называют математическое ожидание квадрата отклонения случайной величины называют математическое ожидание квадрата отклонения случайной величины 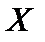 от ее математического ожидания от ее математического ожидания  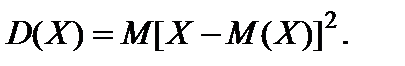 Из этого определения следует, что для дискретной случайной величины Из этого определения следует, что для дискретной случайной величины 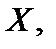 распределенной по закону (10), дисперсия распределенной по закону (10), дисперсия 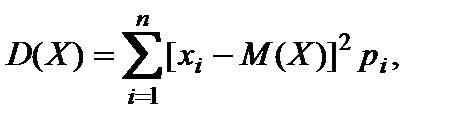 (18),а для непрерывной случайной величины (18),а для непрерывной случайной величины 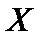 с плотностью вероятностей с плотностью вероятностей  — —  при условии, что этот интеграл сходится.Из свойств математического ожидания и определения дисперсии нетрудно получить формулу при условии, что этот интеграл сходится.Из свойств математического ожидания и определения дисперсии нетрудно получить формулу  (19),то есть дисперсия случайной величины (19),то есть дисперсия случайной величины 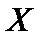 равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания.Свойства дисперсии:1°. Дисперсия постоянной величины равна нулю: равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания.Свойства дисперсии:1°. Дисперсия постоянной величины равна нулю:  2°.Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: 2°.Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат:  3°.Дисперсия алгебраической суммы двух независимых случайных величин 3°.Дисперсия алгебраической суммы двух независимых случайных величин 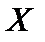 и и 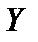 равна сумме их дисперсий: равна сумме их дисперсий:  Дисперсия как мера рассеяния значений случайной величины обладает тем недостатком, что ее размерность не совпадает с размерностью случайной величины (размерность дисперсии — квадрат размерности случайной величины). Поэтому вводится еще одна мера рассеяния (числовая характеристика) с размерностью, совпадающей с размерностью случайной величины. Это так называемое среднее квадратическое отклонение, которое определяется как корень квадратный из дисперсии случайной величины Дисперсия как мера рассеяния значений случайной величины обладает тем недостатком, что ее размерность не совпадает с размерностью случайной величины (размерность дисперсии — квадрат размерности случайной величины). Поэтому вводится еще одна мера рассеяния (числовая характеристика) с размерностью, совпадающей с размерностью случайной величины. Это так называемое среднее квадратическое отклонение, которое определяется как корень квадратный из дисперсии случайной величины 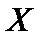 и обозначается через и обозначается через  то есть то есть  Модой дискретной СВ Хназ-т её наиболее вероятное значение, а для непрерывной СВ Х наз-т такое её значение, Мо для которого f(Мо)=мах {f(x)}. Медианойобозн.(Ме) СВ Х наз.такое её значение, для которого вер-ть что Х примет лишнее значение P(X<Me)=P(X>Me). В случае симметрического распределения СВ мода и медиана совпадают с её математическим ожиданием. Началом моментатакого порядка назовём матем.ожидание такой степени n-ой величины: γк=М(Хк). Центральным моментомтакого порядка СВ (Х) назовём Мо такой степени, откл.эт.велич.от её Мо: ϻк=М [X-M(X)]к. Очевидно, что начальный момент 1 порядка –это Мо, а центральный 2-го порядка –это дисперсия. γк=М(Х)=ϻк=D(X). Модой дискретной СВ Хназ-т её наиболее вероятное значение, а для непрерывной СВ Х наз-т такое её значение, Мо для которого f(Мо)=мах {f(x)}. Медианойобозн.(Ме) СВ Х наз.такое её значение, для которого вер-ть что Х примет лишнее значение P(X<Me)=P(X>Me). В случае симметрического распределения СВ мода и медиана совпадают с её математическим ожиданием. Началом моментатакого порядка назовём матем.ожидание такой степени n-ой величины: γк=М(Хк). Центральным моментомтакого порядка СВ (Х) назовём Мо такой степени, откл.эт.велич.от её Мо: ϻк=М [X-M(X)]к. Очевидно, что начальный момент 1 порядка –это Мо, а центральный 2-го порядка –это дисперсия. γк=М(Х)=ϻк=D(X).
|

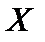 будем обозначать символом[2]
будем обозначать символом[2] 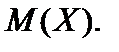 Для дискретной случайной величины
Для дискретной случайной величины 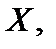 представленной рядом распределения (10), математическое ожидание определяется равенством
представленной рядом распределения (10), математическое ожидание определяется равенством  (17). Пусть
(17). Пусть  Тогда математическое ожидание этой случайной величины, возможные значения которой принадлежат отрезку
Тогда математическое ожидание этой случайной величины, возможные значения которой принадлежат отрезку 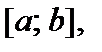 находятся по формуле
находятся по формуле  . Если непрерывная случайная величина может принимать любые значения числовой прямой, то
. Если непрерывная случайная величина может принимать любые значения числовой прямой, то  . Свойства математического ожидания: 1°. Математическое ожидание постоянной величины равно этой постоянной:
. Свойства математического ожидания: 1°. Математическое ожидание постоянной величины равно этой постоянной:  2°.Постоянный множитель можно выносить за знак математического ожидания:
2°.Постоянный множитель можно выносить за знак математического ожидания: 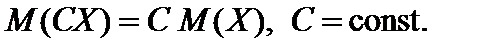 3°.Математическое ожидание алгебраической суммы двух случайных величин
3°.Математическое ожидание алгебраической суммы двух случайных величин 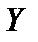 равно алгебраической сумме их математических ожиданий:
равно алгебраической сумме их математических ожиданий:  4°. Математическое ожидание произведения двух независимых[3] случайных величин
4°. Математическое ожидание произведения двух независимых[3] случайных величин  Математическое ожидание является числом постоянным, независящим от опыта и характеризующим определенное свойство случайной величины — устойчивость среднего арифметического значений случайной величины, полученных в результате испытаний. Однако этой числовой характеристики не всегда бывает достаточно.
Математическое ожидание является числом постоянным, независящим от опыта и характеризующим определенное свойство случайной величины — устойчивость среднего арифметического значений случайной величины, полученных в результате испытаний. Однако этой числовой характеристики не всегда бывает достаточно.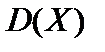 случайной величины
случайной величины 
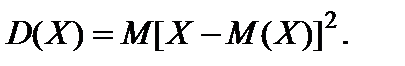 Из этого определения следует, что для дискретной случайной величины
Из этого определения следует, что для дискретной случайной величины 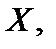 распределенной по закону (10), дисперсия
распределенной по закону (10), дисперсия 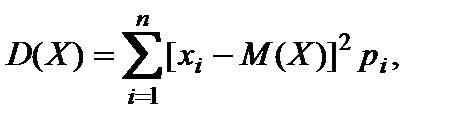 (18),а для непрерывной случайной величины
(18),а для непрерывной случайной величины 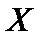 с плотностью вероятностей
с плотностью вероятностей  —
—  при условии, что этот интеграл сходится.Из свойств математического ожидания и определения дисперсии нетрудно получить формулу
при условии, что этот интеграл сходится.Из свойств математического ожидания и определения дисперсии нетрудно получить формулу  (19),то есть дисперсия случайной величины
(19),то есть дисперсия случайной величины  2°.Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат:
2°.Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат:  3°.Дисперсия алгебраической суммы двух независимых случайных величин
3°.Дисперсия алгебраической суммы двух независимых случайных величин  Дисперсия как мера рассеяния значений случайной величины обладает тем недостатком, что ее размерность не совпадает с размерностью случайной величины (размерность дисперсии — квадрат размерности случайной величины). Поэтому вводится еще одна мера рассеяния (числовая характеристика) с размерностью, совпадающей с размерностью случайной величины. Это так называемое среднее квадратическое отклонение, которое определяется как корень квадратный из дисперсии случайной величины
Дисперсия как мера рассеяния значений случайной величины обладает тем недостатком, что ее размерность не совпадает с размерностью случайной величины (размерность дисперсии — квадрат размерности случайной величины). Поэтому вводится еще одна мера рассеяния (числовая характеристика) с размерностью, совпадающей с размерностью случайной величины. Это так называемое среднее квадратическое отклонение, которое определяется как корень квадратный из дисперсии случайной величины  то есть
то есть  Модой дискретной СВ Хназ-т её наиболее вероятное значение, а для непрерывной СВ Х наз-т такое её значение, Мо для которого f(Мо)=мах {f(x)}. Медианойобозн.(Ме) СВ Х наз.такое её значение, для которого вер-ть что Х примет лишнее значение P(X<Me)=P(X>Me). В случае симметрического распределения СВ мода и медиана совпадают с её математическим ожиданием. Началом моментатакого порядка назовём матем.ожидание такой степени n-ой величины: γк=М(Хк). Центральным моментомтакого порядка СВ (Х) назовём Мо такой степени, откл.эт.велич.от её Мо: ϻк=М [X-M(X)]к. Очевидно, что начальный момент 1 порядка –это Мо, а центральный 2-го порядка –это дисперсия. γк=М(Х)=ϻк=D(X).
Модой дискретной СВ Хназ-т её наиболее вероятное значение, а для непрерывной СВ Х наз-т такое её значение, Мо для которого f(Мо)=мах {f(x)}. Медианойобозн.(Ме) СВ Х наз.такое её значение, для которого вер-ть что Х примет лишнее значение P(X<Me)=P(X>Me). В случае симметрического распределения СВ мода и медиана совпадают с её математическим ожиданием. Началом моментатакого порядка назовём матем.ожидание такой степени n-ой величины: γк=М(Хк). Центральным моментомтакого порядка СВ (Х) назовём Мо такой степени, откл.эт.велич.от её Мо: ϻк=М [X-M(X)]к. Очевидно, что начальный момент 1 порядка –это Мо, а центральный 2-го порядка –это дисперсия. γк=М(Х)=ϻк=D(X).