Плотность вероятностей СВ и ее свойства.

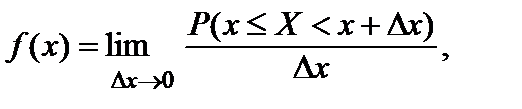При изучении непрерывных случайных величин одним из основных является понятие плотности вероятностей. Плотностью вероятностей или дифференциальной функцией распределения называется предел     (14) при условии, что он существует. 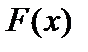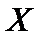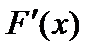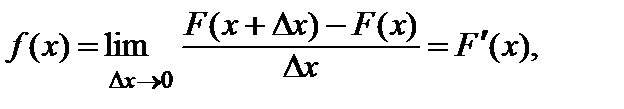Пусть — функция распределения случайной величины  и существует производная  в любой точке  Тогда в силу свойства 3^° функции распределения  равенство (14) равносильно соотношению  то есть плотность вероятностей равна производной от функции распределения. Поэтому  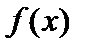часто называют дифференциальной функцией распределения. Плотность вероятностей обладает следующими свойствами:  1^°. Функция 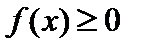— неотрицательная, то есть . 2^°.Функция распределения  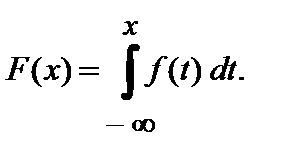выражается через плотность вероятностей  формулой (В этой связи функцию  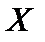называют еще интегральной функцией распределения). 3^°.Вероятность попадания значений случайной величины  в полуинтервал  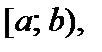равна определенному интегралу по отрезку  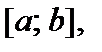то есть  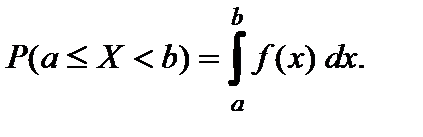                        (15). Геометрически равенство (15) означает, что вероятность  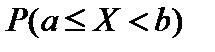равна площади криволинейной трапеции, ограниченной графиком функции  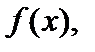осью 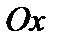 и отрезками прямых 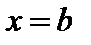 (рис. 3).

4^°.Несобственный интеграл от плотности вероятностей 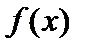 в пределах от  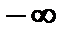до 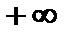 равен единице:  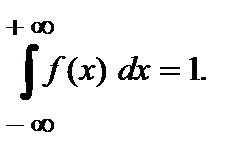 (16). Если все значения случайной величины  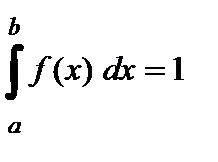заключены в отрезке  то равенство (16) можно записать в виде . График функции  называют кривой плотности распределения вероятностей случайной величины  или просто кривой распределения.