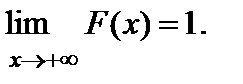Студопедия
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
|
Закон распределения СВ. Функция распределения СВ и ее свойства.
Понятие случайной величины (СВ). Виды СВ. Примеры.
Одним из основных понятий в теории вероятностей является понятие случайной величины, под которой будем понимать некоторую величину, принимающую в зависимости от случая те или иные значения с определенными вероятностями. Различают два вида случайных величин: дискретные и непрерывные. Дискретной назовем случайную величину, принимающую изолированные друг от друга значения, которые можно пронумеровать. Обычно дискретная случайная величина используется при описании измерений, принимающих целочисленные значения (например, количество отличных оценок у студентов одной группы на экзамене; число растений спелой ржи на 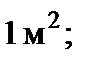 количество деталей высокого качества, сошедших с конвейера в течение смены и т. д.).Непрерывной будемназывать случайную величину, возможные значения которой заполняют некоторый числовой промежуток (например, глубина заделки семян при посеве; погрешность при измерении той или иной величины; периметр перпендикулярного сечения ствола дерева и т. д.).Случайные величины обозначают последними прописными буквами латинского алфавита количество деталей высокого качества, сошедших с конвейера в течение смены и т. д.).Непрерывной будемназывать случайную величину, возможные значения которой заполняют некоторый числовой промежуток (например, глубина заделки семян при посеве; погрешность при измерении той или иной величины; периметр перпендикулярного сечения ствола дерева и т. д.).Случайные величины обозначают последними прописными буквами латинского алфавита 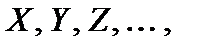 а принимаемые ими значения — соответствующими строчными буквами а принимаемые ими значения — соответствующими строчными буквами  .Примерами СВ могут быть: 1. Кол-во отличных оценок у студентов 1 группы на экзамене, 2. Число растений спелой ржи на 1 м2, 3. Сумма выигрыша в лотерею, 4. Глубина заделки семян при посеве, 5. Погрешность при измерении той или иной величины и т.д. .Примерами СВ могут быть: 1. Кол-во отличных оценок у студентов 1 группы на экзамене, 2. Число растений спелой ржи на 1 м2, 3. Сумма выигрыша в лотерею, 4. Глубина заделки семян при посеве, 5. Погрешность при измерении той или иной величины и т.д.
Закон распределения СВ. Функция распределения СВ и ее свойства.
 Всякое соотношение, устанавливающее связь между значениями случайной величины и соответствующими им вероятностями, будем называть законом распределенияслучайной величины.Закон распределения может иметь разные формы.Закон распределения дискретной случайной величины обычно задается рядом распределения, под которым понимают таблицу, где перечислены значения случайной величины Всякое соотношение, устанавливающее связь между значениями случайной величины и соответствующими им вероятностями, будем называть законом распределенияслучайной величины.Закон распределения может иметь разные формы.Закон распределения дискретной случайной величины обычно задается рядом распределения, под которым понимают таблицу, где перечислены значения случайной величины  и соответствующие им вероятности и соответствующие им вероятности 
 Здесь Здесь 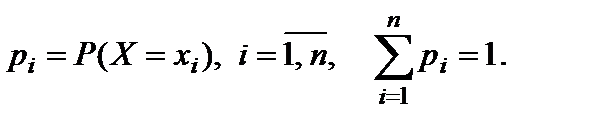 Графическое изображение ряда распределения (см. рис. 1) представляет собой ломанную линию, соединяющую точки Графическое изображение ряда распределения (см. рис. 1) представляет собой ломанную линию, соединяющую точки 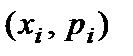 и называется многоугольником (полигоном) распределения. Универсальным способом задания случайной величины и называется многоугольником (полигоном) распределения. Универсальным способом задания случайной величины  является задание ее функции распределения является задание ее функции распределения 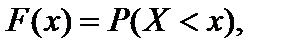 (11), задающей вероятность события (11), задающей вероятность события  состоящего в том, что случайная величина состоящего в том, что случайная величина  примет значение, меньшее примет значение, меньшее 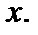 Геометрически равенство (11) можно истолковать так: если значения случайной величины Геометрически равенство (11) можно истолковать так: если значения случайной величины  рассматривать как точки числовой прямой рассматривать как точки числовой прямой  то функция распределения то функция распределения 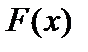 определяет вероятность попадания случайной точки определяет вероятность попадания случайной точки 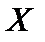 левее точки левее точки 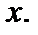 Функция распределения Функция распределения 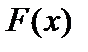 для дискретной случайной величины для дискретной случайной величины 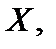 заданной рядом распределения (10), имеет вид заданной рядом распределения (10), имеет вид  (12)где неравенство под знаком суммы указывает на то, что суммируются вероятности тех значений, которые меньше (12)где неравенство под знаком суммы указывает на то, что суммируются вероятности тех значений, которые меньше 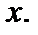 Функция распределения (12) для дискретной случайной величины Функция распределения (12) для дискретной случайной величины 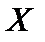 является разрывной и представляет собой ступенчатую линию (рис. 2). Функция распределения (11) обладает следующими свойствами: 1°. Все значения функции распределения является разрывной и представляет собой ступенчатую линию (рис. 2). Функция распределения (11) обладает следующими свойствами: 1°. Все значения функции распределения 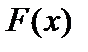 принадлежат отрезку принадлежат отрезку 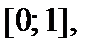 то есть то есть 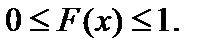 2°. Функция распределения 2°. Функция распределения 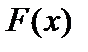 является неубывающей, то есть является неубывающей, то есть  для всех значений для всех значений  3°.Вероятность того, что случайная величина 3°.Вероятность того, что случайная величина 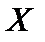 примет значение из полуинтервала примет значение из полуинтервала 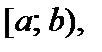 равна разности значений ее функции распределения на концах этого промежутка равна разности значений ее функции распределения на концах этого промежутка 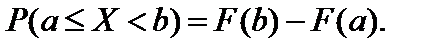 (13). 4°.Функция (13). 4°.Функция 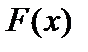 непрерывна слева при любом непрерывна слева при любом 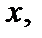 то есть то есть  5°.Функция 5°.Функция 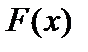 определена на всей числовой прямой, при этом определена на всей числовой прямой, при этом 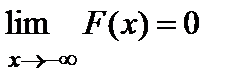 и и 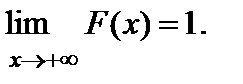
|


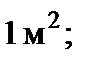 количество деталей высокого качества, сошедших с конвейера в течение смены и т. д.).Непрерывной будемназывать случайную величину, возможные значения которой заполняют некоторый числовой промежуток (например, глубина заделки семян при посеве; погрешность при измерении той или иной величины; периметр перпендикулярного сечения ствола дерева и т. д.).Случайные величины обозначают последними прописными буквами латинского алфавита
количество деталей высокого качества, сошедших с конвейера в течение смены и т. д.).Непрерывной будемназывать случайную величину, возможные значения которой заполняют некоторый числовой промежуток (например, глубина заделки семян при посеве; погрешность при измерении той или иной величины; периметр перпендикулярного сечения ствола дерева и т. д.).Случайные величины обозначают последними прописными буквами латинского алфавита 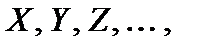 а принимаемые ими значения — соответствующими строчными буквами
а принимаемые ими значения — соответствующими строчными буквами  .Примерами СВ могут быть: 1. Кол-во отличных оценок у студентов 1 группы на экзамене, 2. Число растений спелой ржи на 1 м2, 3. Сумма выигрыша в лотерею, 4. Глубина заделки семян при посеве, 5. Погрешность при измерении той или иной величины и т.д.
.Примерами СВ могут быть: 1. Кол-во отличных оценок у студентов 1 группы на экзамене, 2. Число растений спелой ржи на 1 м2, 3. Сумма выигрыша в лотерею, 4. Глубина заделки семян при посеве, 5. Погрешность при измерении той или иной величины и т.д. Всякое соотношение, устанавливающее связь между значениями случайной величины и соответствующими им вероятностями, будем называть законом распределенияслучайной величины.Закон распределения может иметь разные формы.Закон распределения дискретной случайной величины обычно задается рядом распределения, под которым понимают таблицу, где перечислены значения случайной величины
Всякое соотношение, устанавливающее связь между значениями случайной величины и соответствующими им вероятностями, будем называть законом распределенияслучайной величины.Закон распределения может иметь разные формы.Закон распределения дискретной случайной величины обычно задается рядом распределения, под которым понимают таблицу, где перечислены значения случайной величины  и соответствующие им вероятности
и соответствующие им вероятности 
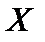

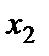
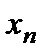

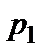


 Здесь
Здесь 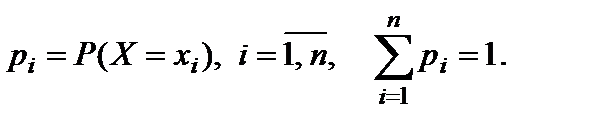 Графическое изображение ряда распределения (см. рис. 1) представляет собой ломанную линию, соединяющую точки
Графическое изображение ряда распределения (см. рис. 1) представляет собой ломанную линию, соединяющую точки 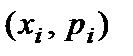 и называется многоугольником (полигоном) распределения. Универсальным способом задания случайной величины
и называется многоугольником (полигоном) распределения. Универсальным способом задания случайной величины 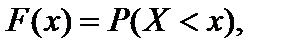 (11), задающей вероятность события
(11), задающей вероятность события  состоящего в том, что случайная величина
состоящего в том, что случайная величина 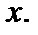 Геометрически равенство (11) можно истолковать так: если значения случайной величины
Геометрически равенство (11) можно истолковать так: если значения случайной величины 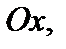 то функция распределения
то функция распределения 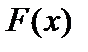 определяет вероятность попадания случайной точки
определяет вероятность попадания случайной точки 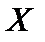 левее точки
левее точки 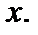 Функция распределения
Функция распределения 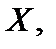 заданной рядом распределения (10), имеет вид
заданной рядом распределения (10), имеет вид  (12)где неравенство под знаком суммы указывает на то, что суммируются вероятности тех значений, которые меньше
(12)где неравенство под знаком суммы указывает на то, что суммируются вероятности тех значений, которые меньше 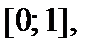 то есть
то есть 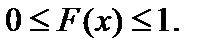 2°. Функция распределения
2°. Функция распределения  для всех значений
для всех значений  3°.Вероятность того, что случайная величина
3°.Вероятность того, что случайная величина 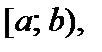 равна разности значений ее функции распределения на концах этого промежутка
равна разности значений ее функции распределения на концах этого промежутка 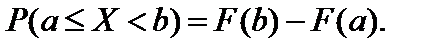 (13). 4°.Функция
(13). 4°.Функция 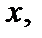 то есть
то есть  5°.Функция
5°.Функция 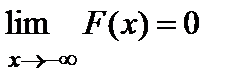 и
и