
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Математическое ожидание функции одного случайного аргумента.Пусть Y = φ(X) – функция случайного аргумента Х, и требуется найти ее математическое ожидание, зная закон распределения Х. 1) Если Х – дискретная случайная величина, то
2) Если Х – непрерывная случайная величина, то M(Y) можно искать по-разному. Если известна плотность распределения g(y), то 21. Функция двух случайных аргументов. Распределение функции Z=Х+У для дискретных независимых СВ Х и У.(тетр) Если каждой паре возможных значений случайных величии X и У соответствует одно возможное значение случайной величины Z, то Z называют функцией двух случайных аргументов X и Y и пишут Z=φ(X,Y). Если X и Y—дискретные независимые случайные величины, то, для того чтобы найти распределение функции Z=X+Y, надо найти все возможные значения Z, для чего достаточно сложить каждое возможное значение X со всеми возможными значениями Y; вероятности найденных возможных значений Z равны произведениям вероятностей складываемых значений X и Y. Если X н Y—непрерывные независимые случайные величины, то плотность распределения g(z) суммы Z = X+Y (при условии, что плотность распределения хотя бы одного из аргументов задана в интервале (— оо, оо) одной формулой) может быть найдена по формуле  X 1 3 Y 2 4 , Р 0,3 0,7 Р 0,6 0,4 Найти распределение случайной величины Z = X + K. Решение. Для того чтобы составить распределение величины Z=X+Y, надо найти все возможные значения Z и их вероятности. Возможные значения Z есть суммы каждого возможного значения X со всеми возможными значениями Y: Z1 = 1+2=3; z2 = 1+4 = 5; z3=3+2 = 5; z4 = 3+4 = 7. Найдем вероятности этих возможных значений. Для того чтобы Z=3, достаточно, чтобы величина X приняла значение x1= l и величина К—значение y1=2. Вероятности этих возможных значений, как следует из данных законов распределения, соответственно равны 0,3 и 0,6. Так как аргументы X и Y независимы, то события Х =1 и Y=2 независимы н, следовательно, вероятность их совместного наступления (т. е. вероятность события Z = 3) по теореме умножения раина 0,3*0,6=0,18. Аналогично найдем: Я B=!-f4 = 5) = 0,3 0,4 = 0,12; P(Z = 34-2 = 5) =0,7 0.6 = 0,42; P(Z = 3-Й = 7) =0,7-0,4 = 0.28. Напишем искомое распределение, сложив предварительно вероятности несовместных событий Z = z2 = 5, Z=z3 = 5 (0,12+0,42=0,54): Z 3 5 7 ; Р 0,18 0,54 0,28 . Контроль: 0,18 + 0,54+0,28 = 1. |
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 301. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
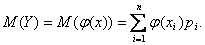

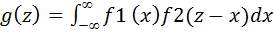 , либо по равносильной формуле
, либо по равносильной формуле 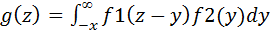 , где f1 и f2—плотности распределения аргументов; если возможные значения аргументов неотрицательны, то плотность распределения g(z) величины Z=X + Y находят по формуле
, где f1 и f2—плотности распределения аргументов; если возможные значения аргументов неотрицательны, то плотность распределения g(z) величины Z=X + Y находят по формуле 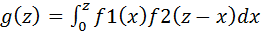 , либо по равносильной формуле
, либо по равносильной формуле 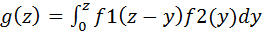 . В том случае, когда обе плотности f1(x) и f2(y) заданы на конечных интервалах, для отыскания плотности g(z) величины Z = X+Y целесообразно сначала найти функцию распределения G(z), а затем продифференцировать ее по z: g(z)=G’(z). Если X и Y—независимые случайные величины, заданные соответствующими плотностями распределения f1(x) и f2(y), то вероятность попадания случайной точки (X, Y) в область D равна двойному интегралу по этой области от произведения плотностей распределения: Р [(Х, У)сD] =
. В том случае, когда обе плотности f1(x) и f2(y) заданы на конечных интервалах, для отыскания плотности g(z) величины Z = X+Y целесообразно сначала найти функцию распределения G(z), а затем продифференцировать ее по z: g(z)=G’(z). Если X и Y—независимые случайные величины, заданные соответствующими плотностями распределения f1(x) и f2(y), то вероятность попадания случайной точки (X, Y) в область D равна двойному интегралу по этой области от произведения плотностей распределения: Р [(Х, У)сD] = 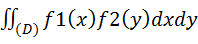 . Дискретные независимые случайные величины X и Y заданы распределениями:
. Дискретные независимые случайные величины X и Y заданы распределениями: