
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Кореляційний момент (коваріація, коефіцієнт кореляції). Властивості cov xy, rxy.Корреляционный момент есть характеристика системы случайных величин, описывающая, помимо рассеивания величин Х и Y, еще и связь между ними. Для того, чтобы убедиться в этом отметим, что корреляционный момент независимых случайных величин равен нулю. Заметим, что корреляционный момент характеризует не только зависимость величин, но и их рассеивание. Поэтому для характеристики связи между величинами (Х;Y) в чистом виде переходят от момента Kxy к характеристике
где σx, σy - средние квадратичные отклонения величин Х и Y. Эта характеристика называется коэффициентом корреляции величин Х и Y. Случайные величины, для которых rxy=0, называют некоррелированными (несвязанными).
Нерівність Чебишева.(доведення). Нехай
Звідси одержуємо,

Теорема Чебишева.(доведення). Нехай 1.M(Xі)>= aі 2.D(Xі )<= с Для всіх і=1,2,3…..n Якщо випадкові величини у послідовності Ця теорема є законом великих чисел ,так само як і центральна гранична теорема
Теорема Бернуллі.(доведення). Нехай проводиться n незалежних повторних випробувань, у кожному з яких імовірність настання події А дорівнює р.Якщо ймовірність появи випадкової події А в кожному з незалежних випробувань n є величиною сталою і дорівнює P,то при необмеженому збільшенні числа експериментів n→∞ Імовірність відхилення відносної частоти появи випадкової події W(A) від імовірності p ,взятої за абсолютною величиною на ε(ε>0) прямуватиме до одиниці зі зростанням n ,що можна записати так:
де Наведена теорема є законом великих чисел ,так само як і центральна гранична теорема |
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 318. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
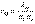
 ,
,
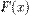 - функція розподілу змінної
- функція розподілу змінної 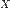 . Тоді:
. Тоді: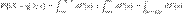
 З того, що
З того, що 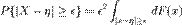 одержуємо твердження
одержуємо твердження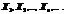 послідовність незалежних випадкових величин ,які задовольняють умовам:
послідовність незалежних випадкових величин ,які задовольняють умовам: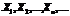 незалежні, мають скінченні математичні сподівання і рівномірно обмежені дисперсії
незалежні, мають скінченні математичні сподівання і рівномірно обмежені дисперсії 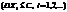 , то до послідовності (1) можна застосувати закон великих чисел. Це означає що середне арифметичне достатньо великої кількості незалежних випадкових величин дуже мало відрізняється від середнього арифметичного їхніх математичних сподівань ,взятого за абсолютним значенням .
, то до послідовності (1) можна застосувати закон великих чисел. Це означає що середне арифметичне достатньо великої кількості незалежних випадкових величин дуже мало відрізняється від середнього арифметичного їхніх математичних сподівань ,взятого за абсолютним значенням .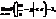
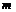 — частота події А у даних випробуваннях. Таким чином при необмеженому збільшенні числа незалежних випробувань за схемою Бернулі відносна частота дуже мало відрізняється від ймовірності .
— частота події А у даних випробуваннях. Таким чином при необмеженому збільшенні числа незалежних випробувань за схемою Бернулі відносна частота дуже мало відрізняється від ймовірності .