
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Розподіл Фішера – Снедекора.Якщо випадкові величини
Для розподілу Фішера складено таблиці, в яких для відповідної кількості ступенів волі для ймовірностей
Система двох дискретних випадкових величин. Числові характеристики двомірної випадкової величини.
Система двох неперервних випадкових величин. Функції розподілу F(x,y) та її властивості. Функція розподілу
Функція розподілу має такі властивості:
Функції За допомогою функції розподілу можна подати ймовірність потрапляння випадкової точки у прямокутник, сторони якого паралельні осям координат:
Якщо розглядається система неперервних випадкових вели-чин, то для неї визначається щільність розподілу 1) 2) Імовірність потрапляння випадкової точки
Функція розподілу системи двох випадкових величин виражається через щільність розподілу:
Скориставшись властивостями функції розподілу системи неперервних величин, можна знайти щільності розподілу величин, які входять до цієї системи: 
19.Сукупність випадкових величин
Якщо елементи цієї матриці поділимо на добуток
Щільність розподілу системи двох випадкових величин. Для двовимірної випадкової величини
де Властивості щільності розподілу : 1. 2. 3. 4. 5. Умовні закони розподілу системи двох випадкових величин. Числові характеристики. (Умовне математичне сподівання). |
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 348. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 незалежні і мають
незалежні і мають  — розподіл відповідно з
— розподіл відповідно з  ступенями волі, то випадкова величина
ступенями волі, то випадкова величина  має розподіл Фішера з
має розподіл Фішера з  ступенями волі. Щільність цього розподілу подається формулою:
ступенями волі. Щільність цього розподілу подається формулою: Щільність розподілу Фішера має графік, зображений на
Щільність розподілу Фішера має графік, зображений на
 наведено значення
наведено значення  –
– 

 системи двох випадкових величин визначає ймовірність спільного настання двох подій:
системи двох випадкових величин визначає ймовірність спільного настання двох подій: 
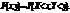 Геометрично функцію розподілу можна інтерпретувати як імовірність потрапляння випадкової точки в нескінченний прямокутник із вершиною
Геометрично функцію розподілу можна інтерпретувати як імовірність потрапляння випадкової точки в нескінченний прямокутник із вершиною  обмежений згори і праворуч
обмежений згори і праворуч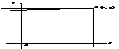

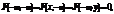

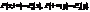
 визначають закони розподілу для випадкових величин
визначають закони розподілу для випадкових величин  які входять до системи.
які входять до системи.

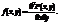 При цьому
При цьому  має такі властивості:
має такі властивості:
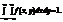
 у довільну область D подається формулою:
у довільну область D подається формулою: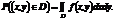


 які розглядаються спільно, називається системою
які розглядаються спільно, називається системою  випадкових величин.Для системи випадкових величин
випадкових величин.Для системи випадкових величин 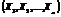 числові характеристики задаються вектором математичних сподівань
числові характеристики задаються вектором математичних сподівань  і кореляційною матрицею:
і кореляційною матрицею:
 , дістанемо матрицю, складену з коефіцієнтів кореляції:
, дістанемо матрицю, складену з коефіцієнтів кореляції:
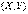 дискретного та неперервного типу функції розподілу відповідно такі:
дискретного та неперервного типу функції розподілу відповідно такі: ,
, 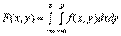 ,
, — щільність розподілу ймовірностей випадкової величини
— щільність розподілу ймовірностей випадкової величини  .
.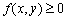 ;
; ;
; ;
;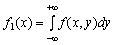 ;
; .
.