Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Закон розподілу дискретної випадкової величини.Законом распределения дискретной случайной величины называют соответствие между возможными значениями случайной величины и вероятностями их появления. Закон распределения можно задать таблично, аналитически (в виде формулы) или графически (в виде многоугольника распределения). Рассмотрим случайную величину X, которая принимает значения x1, x2, x3 ... xn с некоторой вероятностью pi, где i = 1.. n. Сумма вероятностей piравна 1.
Таблица соответствия значений случайной величины и их вероятностей вида
называется рядом распределения дискретной случайной величины или просто рядом распределения. Эта таблица является наиболее удобной формой задания дискретной случайной величины.
Щільність ймовірностей, її властивості. Плотность вероятности (плотность распределения вероятностей) случайной величины X - ф-ция р (х)такая, что
Если р(х)непрерывна, то при достаточно малых
и, если F(x)дифференцируема,
Случайные величины, имеющие П. в., наз. непрерывно распределёнными случайными величинами, а их распределения - непрерывными (точнее, абсолютно непрерывными) распределениями.
29. Алгебраїчні дії над дискретними випадковими величинами: множення на константу, додавання константи, возведення в квадрат. 
30. Алгебраїчні дії над дискретними випадковими величинами: множення та додавання незалежних випадкових величин.
Математичне сподівання та його властивості для дискретної випадкової величини. Математичним сподіванням, або середнім значенням, МХ випадкової величини, називається ряд 1) 2) 3) 4) Математичним сподіванням дискретної випадкової величини називається сума добутку всіх її значень на відповідні їм ймовірності:
де
Математичне сподівання та його властивості для неперервної випадкової величини. Математичним сподіванням, або середнім значенням, МХ випадкової величини, називається ряд 5) 6) 7) 8)
|
||||||||||||||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 315. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
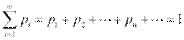
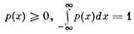 и при любых а < b вероятность события а < X < b равна
и при любых а < b вероятность события а < X < b равна
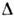 х вероятность неравенства х < X < х +
х вероятность неравенства х < X < х +  х приближённо равна р(х)
х приближённо равна р(х) 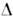 х (с точностью до малых более высокого порядка). Ф-ция распределения F(x)случайной величины X, имеющей плотность, связана с П. в. соотношениями
х (с точностью до малых более высокого порядка). Ф-ция распределения F(x)случайной величины X, имеющей плотность, связана с П. в. соотношениями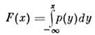
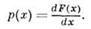
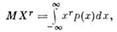
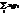 (для дискретних випадкових величин) і інтеграл
(для дискретних випадкових величин) і інтеграл 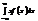 (для неперервних випадкових величин), якщо вони абсолютно збіжні. Математичне сподівання має такі властивості:
(для неперервних випадкових величин), якщо вони абсолютно збіжні. Математичне сподівання має такі властивості: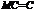 (С — стала);
(С — стала);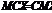 ;
;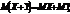
 якщо Х і Y — незалежні випадкові величини.
якщо Х і Y — незалежні випадкові величини.