
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Нормальний закон розподілу неперервної випадкової величини.Нормальний закон розподілу задається щільністю
Часто застосовується також формула:
Ймовірність влучення нормально розподіленої величини в заданий інтервал Зная плотность распределения, можно вычислить вероятность того, что непрерывная случайная величина примет значение, принадлежащее заданному интервалу. Вычисление основано на следующей теореме. Теорема. Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (а, b), равна определенному интегралу от плотности распределения, взятому в пределах от а до b: Р(а<Х<b) =
Доказательство. Р(а ≤Х<b) = F(b) — F(a). По формуле Ньютона — Лейбница, F(b) — F(a)= Таким образом, Р(а
Так как Р(а ≤Х<b) = Р(а<Х<b),то окончательно получим Р(а<Х<b) = Геометрически полученный результат можно истолковать так: вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (а,b), равна площади криволинейной трапеции, ограниченной осью Ох, кривой распределения f (х)и прямыми х =а и х=b. Замечание. В частности, если f (х)— четная функция и концы интервала симметричны относительно начала координат, то Р(-а<Х<a) = Р(|Х|<a) =2
46. Ймовірність заданого відхилення. Правило 3ᵟ  Очевидно, события, состоящие в осуществлении неравенств | X — а|<и ||Х—а|≥, — противоположные. Поэтому, если вероятность осуществления неравенства | X — а| < равна р, то вероятность неравенства |Х—а| Преобразуем формулу
Р (| X — а |< ) = 2Ф ( /) положив = t. В итоге получим Р (| X — а |< t) = 2Ф (t). Если t = 3 и, следовательно, t =3 то Р (| X—а |< 3) = 2Ф (3) = 2 * 0,49865 = 0,9973, т, е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973. Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0,0027. Это означает, что лишь в 0,27% случаев так может произойти. Такие события исходя из принципа невозможности маловероятных событий можно считать практически невозможными. В этом и состоит сущность правила трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения. На практике правило трех сигм применяют так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то есть основание предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.
Композиція неперервних випадкових величин. Стійкість розподілу
Розподіл Хи-квадрат. Розглядаємо послідовність Якщо Графік щільності розподілу зображено на рис. 3.3.
Для розподілу M(X)=n. D(X)=2n.
Розподіл Ст’юдента . Розподіл Стьюдента з n cтупенями волі має випадкова величина
Складено таблиці розподілу Стьюдента, здебільшого виду M(Z)=0.
|
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 319. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
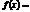
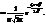 Параметри
Параметри  , які входять до виразу щільності розподілу, є відповідно математичним сподіванням та середнім квадратичним відхиленням випадкової величини. Нормальний закон розподілу широко застосовується в математичній статистиці. Для обчислення ймовірності потрапляння випадкової величини, розподіленої нормально, на проміжок використовується функція Лапласа:
, які входять до виразу щільності розподілу, є відповідно математичним сподіванням та середнім квадратичним відхиленням випадкової величини. Нормальний закон розподілу широко застосовується в математичній статистиці. Для обчислення ймовірності потрапляння випадкової величини, розподіленої нормально, на проміжок використовується функція Лапласа: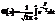

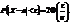

 .
.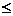 Х<b) =
Х<b) = 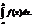
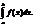
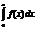
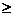 равна 1—р.
равна 1—р.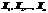 попарно незалежних випадкових величин, які розподілені нормально з нульовими математичними сподіваннями і одиничними дисперсіями.
попарно незалежних випадкових величин, які розподілені нормально з нульовими математичними сподіваннями і одиничними дисперсіями.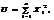 то ця сума має розподіл
то ця сума має розподіл 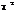 з
з  ступенями волі. Щільність розподілу
ступенями волі. Щільність розподілу 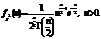 Числові характеристики розподілу:
Числові характеристики розподілу: 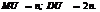 До виразу щільності розподілу входить гамма-функція
До виразу щільності розподілу входить гамма-функція 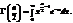

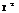 складено таблиці виду
складено таблиці виду 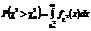 для кількості ступенів волі від 1 до 30. У таблицях для заданих значень імовірностей (здебільшого
для кількості ступенів волі від 1 до 30. У таблицях для заданих значень імовірностей (здебільшого 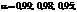 0,9; 0,8; 0,7; 0,5; 0,3; 0,2; 0,1; 0,05; 0,02; 0,01; 0,005; 0,002; 0,001) вказано значення
0,9; 0,8; 0,7; 0,5; 0,3; 0,2; 0,1; 0,05; 0,02; 0,01; 0,005; 0,002; 0,001) вказано значення 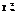 для відповідної кількості ступенів волі. Якщо кількість ступенів волі більша від 30, то розподіл мало відрізняється від нормального з відповідними математичним сподіванням і дисперсією.
для відповідної кількості ступенів волі. Якщо кількість ступенів волі більша від 30, то розподіл мало відрізняється від нормального з відповідними математичним сподіванням і дисперсією. де Х — нормально розподілена величина з нульовим математичним сподіванням і одиничною дисперсією, а
де Х — нормально розподілена величина з нульовим математичним сподіванням і одиничною дисперсією, а 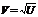 . Випадкова величина
. Випадкова величина 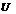 не залежить від Х і має розподіл
не залежить від Х і має розподіл 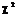 з n ступенями волі. Щільність розподілу
з n ступенями волі. Щільність розподілу 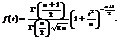 Графік щільності розподілу Стьюдента за зовнішнім виглядом нагадує нормальні криві. Але вони значно повільніше спадають до осі t, якщо
Графік щільності розподілу Стьюдента за зовнішнім виглядом нагадує нормальні криві. Але вони значно повільніше спадають до осі t, якщо 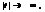 особливо за малих значень n
особливо за малих значень n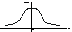
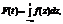 для кількості ступенів волі від 1 до 20. Якщо кількість ступенів волі більша, то можна застосовувати нормальний закон розподілу з нульовим математичним сподіванням і одиничною дисперсією.
для кількості ступенів волі від 1 до 20. Якщо кількість ступенів волі більша, то можна застосовувати нормальний закон розподілу з нульовим математичним сподіванням і одиничною дисперсією.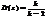 .
.