
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Пуассонівський закон. Числові характеристики.Дискретна випадкова величина має розподіл Пуассона, якщо вона набуває зліченної множини значень Якщо у схемі незалежних повторних випробувань n велике і р або 1 – р прямують до нуля, то біноміальний розподіл апроксимується розподілом Пуассона, коли Ймовірна твірна
Гіпергеометричний закон. Числові характеристики. Гіпергеометричний розподіл описує ймовірність того, що у вибірці з n різних об'єктів, витягнутих із представлення рівноk об'єктів є бракованими. В загальному, якщо випадкова величина X відповідає гіпергеометричному розподілу з параметрами N, D і n, то ймовірність отримання рівно k успіхів визначається формулою:
Ця ймовірність додатня коли k лежить на проміжку між max{ 0, D + n − N } і min{ n, D }. Наведена формула може трактуватися так: існує 
42. Закон рівномірного розподілу на проміжку [a,b]. Якщо ймовірність потрапляння випадкової величини на інтервал пропорційна до довжини інтервалу і не залежить від розташування інтервалу на осі, то вона має рівномірний закон розподілу. Щільність такого розподілу:
Рівномірний закон розподілу легко моделювати. За допомогою функціональних перетворень із величин, розподілених рівномірно, можна діставати величини з довільним законом розподілу. Числові характеристики розподілу:
Пуассонівський (експоненціальний закон) розподілу неперервної випадкової величини. В застосуваннях теорії ймовірностей на практиці: в теорії масового обслуговування, в дослідженні операцій, в теорії надійності мають справу з випадковими величинами, які мають експоненціальний закон розподілу. Випадкова величина x має експоненціальний закон розподілу (показниковий розподіл) із параметром l > 0, якщо вона неперервна та її щільність ймовірностей має такий вигляд:
Тоді функція розподілу ймовірностей буде така:
Таким чином,
|
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 348. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 з імовірностями
з імовірностями  Цей розподіл описує кількість подій, які настають в однакові проміжки часу за умови, що ці події відбуваються незалежно одна від одної зі сталою інтенсивністю. Розподіл Пуассона розглядається як статистична модель для кількості альфа-частинок, що їх випромінює радіоактивне джерело за певний проміжок часу; кількості викликів, які надходять на телефонну станцію за певний період доби; кількості вимог щодо виплати страхових сум за рік; кількості дефектів на однакових пробах речовини і т. ін. Розподіл застосовується в задачах статистичного контролю якості, у теорії надійності, теорії масового обслуговування. Математичне сподівання і дисперсія в цьому розподілі однакові і дорівнюють а. Для цього розподілу складено таблиці щодо різних значень
Цей розподіл описує кількість подій, які настають в однакові проміжки часу за умови, що ці події відбуваються незалежно одна від одної зі сталою інтенсивністю. Розподіл Пуассона розглядається як статистична модель для кількості альфа-частинок, що їх випромінює радіоактивне джерело за певний проміжок часу; кількості викликів, які надходять на телефонну станцію за певний період доби; кількості вимог щодо виплати страхових сум за рік; кількості дефектів на однакових пробах речовини і т. ін. Розподіл застосовується в задачах статистичного контролю якості, у теорії надійності, теорії масового обслуговування. Математичне сподівання і дисперсія в цьому розподілі однакові і дорівнюють а. Для цього розподілу складено таблиці щодо різних значень  (0,1 – 20). У таблицях для відповідних значень а наведено ймовірності
(0,1 – 20). У таблицях для відповідних значень а наведено ймовірності 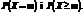



 способів заповнити залишок вибірки (без повернення). Є
способів заповнити залишок вибірки (без повернення). Є  способів вибрати kбракованих об'єктів і
способів вибрати kбракованих об'єктів і  способів заповнити залишок вибірки об'єктами без дефектів.
способів заповнити залишок вибірки об'єктами без дефектів.


 (x > 0).
(x > 0).