
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Функція Гауса її властивості і використання в схемах Бернуллі.У математиці функцією Гауса є функція, що виражається залежністю
Графік функції Гауса є характерною симетричною кривою у формі дзвону, що швидко спадає на нескінченності. Параметр a є висотою піку кривої, b є позицією центру, і c контролює ширину «дзвону». Визначений інтеграл від ґаусової функції дає функцію помилок
Визначений інтеграл з нескінченними границями має властивість
Цей інтеграл рівний 1 тоді і тільки тоді, коли a = 1/(c√(2π)), і в цьому випадку Гаусіан є щільністю нормального розподілу випадкової величини з математичним очікуванням μ=b ідисперсією σ2=c2. При перетворенні Фур'є функції Гауса з параметрами a, b=0 і c отримуємо іншу функцію Гауса, з параметрами ac, b=0 і 1/c. Отже, як частковий випадок, функція Гауса з b=0 і c=1 єінваріантом щодо перетворення Фур'є (вони є власними функціями перетворення Фур'є з власним значенням 1). Функція Лапласа, її властивості і використання в схемі Бернуллі. Випадкові величини, види та способи їх опису. Випадковою величиною назв змінна величина, яка в результаті досвіду може приймати те чи інше числове значення. Випадкові величини бувають виду: дискретні та неперервні. Випадкова величина назв дискретною (перериваною), якщо множина чисел х1,х2…хn, таких що P(X=Xi)=pi≥0; i=1,n і Випадкова величина неперервна, якщо функція розподілу її неперервна, а похідна функції розподілу неперервна в всіх точках, за виключенням кінцевого числа на будь-якому інтервалі.
Функція розподілу ймовірностей для дискретної випадкової величини, її властивості. Закон розподілу ймовірностей можна подати ще в одній формі, яка придатна і для дискретний, і для неперервних випадкових величин, асаме: як функцію розподілу ймовірностей випадкової величини F(x), так звану функцію розподілу. Функцію аргументу x, що визначає ймовірність випадкової події X<x,називають функцією розподілу ймовірностей:  F(x)=P(X<x) Цю функцію можна розглядати як: "у наслідок експерименту випадкова величина може набувати значення, меншого за x" Властивості функції розподілу: · 0 ≤ F(x) ≤ 1 · F(x) є неспадною функцією, тобто: F(x2) ≤ F(x1), якщо x2 > x1 · P(X=xi)=0 Якщо випадкова величина Х є неперервною, то ймовірність того, що вона набуде конкретного можливого значення завжди дорівнює нулю. · lim F(x), при x->- · lim F(x), при x->
Функція розподілу ймовірностей для неперервної випадкової величини, її властивості Если функция распределения Отсюда, в частности, следует, что для любой случайной величины Вероятность того, что значение случайной величины
|
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 427. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
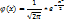



 = lim P(X<x), при x->-
= lim P(X<x), при x->- 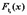 дифференцируема, то более наглядное представление о случайной величине дает плотность вероятности случайной величины
дифференцируема, то более наглядное представление о случайной величине дает плотность вероятности случайной величины 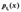 , которая связана с функцией распределения
, которая связана с функцией распределения  и
и  .
. .
. попадает в интервал
попадает в интервал  вычисляется для непрерывной случайной величины по формулам:
вычисляется для непрерывной случайной величины по формулам: или
или 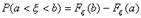 .
.