
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Прості та складні випадкові подій. Простір елементарних подій. Математичні операції над подіями.Використання елементів комбінаторики у теорії ймовірності. Переставленням із n елементів називають такі впорядковані множини з n елементів, які різняться між собою порядком їх розміщення. Кількість таких упорядкованих множин обчислюється за формулою: Pn = n! Розміщенням із n елементів по m (0≤m≤n) називаються такі впорядковані множини, кожна із яких містить m елементів і які відрізняються між собою порядком розташування цих елементів або хоча б одним елементом: Комбінаціямиз n елементів по m (0≤ m≤n) називаються такі множини з m елементів, які різняться між собою хоча б одним елементом:
Теореми додавання ймовірностей. Теорема 1. Ймовірність появи однієї з двох несумісних подій дорівнює сумі ймовірностей цих подій. Р( А È В ) = Р ( А ) + Р ( В ). Наслідок.Ймовірність появи однієї з декількох попарно несумісних подій дорівнює сумі ймовірностей цих подій: Р( А1 È А2 È …È Аn ) = P(A1 + A2+…+ An ). Теорема 2. Нехай А та В - випадкові події. Тоді ймовірність появи хоча б однієї з двох сумісних подій дорівнює сумі ймовірностей цих двох подій без ймовірності їх сумісної появи: R(AÈB) = R(A) + R(B) - R(AÇB) Теорема може бути узагальнена на довільне число сумісних подій. Теорема 3.Нехай А1, А2, …,Аn - випадкові події. Тоді І теорема множення ймовірностей. Теорема множення ймовірностей незалежних подій.Імовірність одночасного настання двох незалежних подій дорівнює добутку ймовірностей цих подій:
 Імовірність появи деяких подій, незалежних у сукупності, обчислюється за формулою:
Залежні та незалежні події. Умовна ймовірність. Події В і С називаються залежними, якщо ймовірність однієї з них змінюється залежно від того, відбулась друга подія чи ні. У противному разі події називаються незалежними. Імовірність події A, визначена за умови, що подія В відбулася, називається умовною і позначається P(A/B). P(A/B)= P(A 1. P(A/B)=0, якщо = 2. P(A/B)=1, якщо =B 3. у решті випадків 0<P(A/B)<1. (3) ІІ теорема множення ймовірностей. Теорема множення ймовірностей залежних подій. Імовірність одночасного настання двох залежних подій дорівнює добутку ймовірності настання однієї з них на умовну ймовірність другої:
Ймовірність появи хоча б раз при n незалежних спробах. Імовірність того, що в n незалежних випробуваннях, у кожному з яких імовірність Р(А) = р, подія А відбудеться m раз, подається так:
Імовірність того, що в результаті n незалежних експериментів подія А з’явиться від mi до mj раз, обчислюється так:
Теорема Байеса (гіпотеза) Подія А може відбутись одночасно з деякою із подій
|
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 394. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 = n! /(n-m)!
= n! /(n-m)!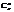 = n! / m!(n-m)!
= n! / m!(n-m)!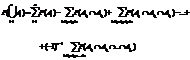
 (1)
(1) (2)
(2) B) / P(B), P(B)
B) / P(B), P(B)  0. Властивості умовної ймовірності:
0. Властивості умовної ймовірності: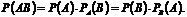
 Формула застосовується, якщо
Формула застосовується, якщо 

 Відомі ймовірності подій
Відомі ймовірності подій  та умовні ймовірності того, що подія А відбудеться. Відомо, що в результаті випробування подія А відбулась. Потрібно з огляду на це переоцінити ймовірності гіпотез
та умовні ймовірності того, що подія А відбудеться. Відомо, що в результаті випробування подія А відбулась. Потрібно з огляду на це переоцінити ймовірності гіпотез  Для цього застосовують формулу Баєса:
Для цього застосовують формулу Баєса: