
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Визначення ймовірності за аксіоматичним підходом.Стр 1 из 12Следующая ⇒ Поняття про випадкові подій; неможливі; вірогідні; сумісні; несумісні подій. Результат, результат випробування називаються подією. 
Класичне визначення ймовірності, її властивості. Частість її визначення та відміна від ймовірності. Класичною імовірністю випадкової події А називається відношення кількості елементарних подій m, які сприяють появі цієї події (становлять множину її елементарних подій), до загальної кількості n рівноможливих елементарних подій, що утворюють простір елементарних подій W: P(A)= m /n. З визначення ймовірності випливають такі її властивості: Властивість 1. Ймовірність достовірної події дорівнює одиниці.В цьому випадку m = n, отже, Властивість 3. Імовірність випадкової події є позитивне число, укладену між нулем і одиницею. В цьому випадку 0 <m <n, значить, 0 <m / n <1, отже, 0 <Р(А) <1. 0 <= Р (A) <1. Частота випадкової події.Нехай W - простір елементарних подій. Розглянемо деякий стохастичний експеримент і подію А, яка спостерігається в цьому експерименті. Повторимо експеримент n раз. Позначимо через Kn(А) - число експериментів, в яких відбулася подія А . Частотою подій А називається відношення
Геометричне визначення ймовірності. Геометричне означення ймовірності. Якщо простір елементарних подій W можна подати у вигляді деякого геометричного предмета, а множину елементарних подій для подій А – як частину цього геометричного образу, то ймовірність події А визначається як відношення мір цих множин P(A)=m(A)/m(W).При цьому вважається, що попадання в деяку частину геометричного образу пропорційна до міри цієї його частини. Статистичною ймовірністю події А називається відношення кількості m випробувань, в яких подія А відбулась, до загальної кількості виконаних випробувань n: W(A)= m /n. Знаходження статистичної ймовірності пов’язане з проведенням n випробувань, тому вона називається ще частістю, або відносною частотою, події.
Визначення ймовірності за аксіоматичним підходом. Ймові́рність — числова характеристика можливості того, що випадкова подія відбудеться в умовах, які можуть бути відтворені необмежену кількість разів. Аксіоматичний підхід, строго сформульований Колмогоровим, будується на припущенні, що імовірності елементарних випадкових подій задані, і зосереджується на визначенні ймовірностей складних подій, що є сукупністю елементарних. Так, наприклад, при підкидуванні шестигранного кубика гральної кості, ймовірності випадіння будь-якого числа, вважаються однаковими й рівними 1/6. Виходячи з цієї аксіоми, теорія ймовірності може розрахувати ймовірність того, що сума чисел на двох костях буде, наприклад, 8. Аксіоми: 3)
|
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 283. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
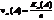 .Частота може бути обчислена лише після того, як проведена серія експериментів, і, взагалі кажучи, частота змінюється, при переході від однієї до інщої серії з n експериментів, або з зміною n. Але, як показує досвід, при достатньо великих n для більшості таких серій експериментів частота зберігає майже постійну величину, причому великі відхилення спостерігаються тим рідше, чим більше n.
.Частота може бути обчислена лише після того, як проведена серія експериментів, і, взагалі кажучи, частота змінюється, при переході від однієї до інщої серії з n експериментів, або з зміною n. Але, як показує досвід, при достатньо великих n для більшості таких серій експериментів частота зберігає майже постійну величину, причому великі відхилення спостерігаються тим рідше, чим більше n.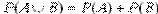 , если А и В несовместны.
, если А и В несовместны.