
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Мера корр. связи. Выборочное корреляционное отношение и его св-ва. простейшие случаи криволинейнойкорр-ции.Целесообразно рассматривать в качестве меры тесноты корреляц-ной зависимости отношение межгрупповой дисперсии к общей, или, что тоже, отношение межгруппового среднего квадратического отклонения к общему среднему квадратическому отклонению. Для оценки тесноты линейной корреляц-ной связи между признаками в выборке служит выборочныйкоэфф-нт корреляции. Для оценки тесноты нелинейной корреляционной связи вводят новые сводные характеристики: Св-ва выбор.корр. отношения: Корреляц-ое отношение удавлетворяет двойному неравенству Если Если Выборочное корреляц-ое отношение не меньше абсолютной величины выборочногокоэфф-нта корреляции: Если выборочное корреляц-ое отношение равно абсолютной величине выборочногокоэфф-нта корреляции, то имеет место точная линейная корреляц-ая зависимость. Если график регрессии Для определения вида функции регрессии строят точки (x;  |
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 330. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 – выборочное корреляционное отношение Y к X
– выборочное корреляционное отношение Y к X  - выборочное корреляционное отношение X к Y . Выборочным корреляц. отношением Y к X называют отношение межгруппового среднего квадратического отклонения к общему среднему квадратическому отклонению признака Y:
- выборочное корреляционное отношение X к Y . Выборочным корреляц. отношением Y к X называют отношение межгруппового среднего квадратического отклонения к общему среднему квадратическому отклонению признака Y:  .
.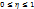 .
. =0, то признак Y с признаком Xкорреляц-ой зависимостью не связан.
=0, то признак Y с признаком Xкорреляц-ой зависимостью не связан. , то признак Y связан с признаком X функциональной зависимостью.
, то признак Y связан с признаком X функциональной зависимостью.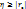 .
. или
или  изображается кривой линией, то корреляцию называют криволинейной. Например, функции регрессии Y на X могут иметь вид:
изображается кривой линией, то корреляцию называют криволинейной. Например, функции регрессии Y на X могут иметь вид:  =ax2+bx+c (параболическая корреляция второго порядка);
=ax2+bx+c (параболическая корреляция второго порядка);  ax3+bx2+cx+d (параболическая корреляция второго порядка).
ax3+bx2+cx+d (параболическая корреляция второго порядка).