
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Точечные и интервальные оценки. Точность оценки, доверительная вероятность(надежность).Доверительный интервал.Точечные оценкиСтатистической оценкойнеизвестного параметра случайной величины X называется функция вариант x1 , x2 , …, xi, …, xn. Несмещенной называют статистическую оценку, математическоеожидание которого равно оцениваемому параметру при любом объеме выборки.Смещеннойназывают статистическую оценку, математическое ожиданиекоторой не равно оцениваемому параметру.Выборочной средней(оценкой математическогоожидания) называют среднее арифметическое наблюдаемых значений количественного признака xi— варианта выборки, ni— частота варианты, k — число наблюдаемых различных значений случайного параметра X . Таким образом, выборочная средняяесть средняя взвешенная значенийпризнака с весами, равными соответствующим частотам.Допустим, что все наблюдаемые значения количественного признака (случайной величины) X выборки разбиты на несколько групп.Рассматривая каждую группу как самостоятельную, можно найти ее среднюю арифметическую.Групповой среднейназывают среднее арифметическое значений признака, принадлежащих группе.Зная групповые средние и объемы группы, можно найти общую среднюю: общая средняя равна средней арифметической групповых средних,взвешенной по объемам групп.Для того, чтобы охарактеризовать рассеяние значений количественногопризнака X совокупности вокруг своего среднего значения xв, вводят характеристику —выборочную дисперсию. Выборочной дисперсиейназывают среднее арифметическое квадратов отклонений наблюдаемых значений количественного признака X от выборочного среднего xв: то есть выборочная дисперсия есть средняя взвешенная квадратовотклонений с весами, равными соответствующим частотам.Кроме выборочной дисперсии для характеристики рассеяния значений  количественного признака X вокруг своего выборочного среднего значенияпользуются характеристикой — выборочным средним квадратическим отклонением.Выборочным средним квадратическим отклонениемвыборочным стандартом) называют квадратный корень из выборочной дисперсии:σ в = Вычисление дисперсии можно упростить, используя формулу:Dв= Выборочная дисперсия Dвявляется смещенной оценкой дисперсии. Для того, чтобы получить несмещенную оценку дисперсии, нужно "исправить" величину Dв. Исправленной выборочной дисперсией S2 называется величина: Исправленным выборочным средним квадратическим отклонениемназывается величина: S = Все рассмотренные выше статистические оценки называются точечными,так как они определяются одним числом. Интервальные оценкиИнтервальнойназывают оценку, которая определяется двумя числами — концами интервала, покрывающего оцениваемый параметр. Доверительнымназывают интервал длиной 2δ , который с заданной вероятностью (надежностью) γ покрывает оцениваемый параметр. Величина δ , равна половине доверительного интервала, называется точностью оценки.
|
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 302. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 =
= 
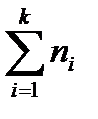 — объем выборки,
— объем выборки, =
= 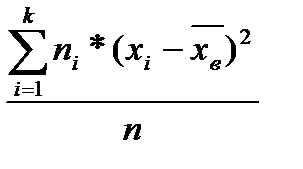

 .
.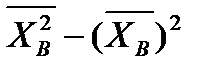 .
. =
= 
 .
.