
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Построение нормальной кривой по опытным данным. Оценка отклонения эмпирического распределения от нормального. Эмпирические асимметрия и эксцесс.Один из способов построения нормальной кривой по данным наблюдений состоит в следующем: находят находят ординаты строят точки (xi, yi) в прямоугольной системе координат и соединяют их плавной кривой. Близость выравнивающих частот к наблюдаемым подтверждает правильность допущения о том, что обследуемый признак распределен нормально. Для того, чтобы уверенно считать, что данные наблюдений свидетельствуют о нормальном распределении признака, пользуются специальными правилами (их называют критериями согласия). Для оценки отклонения эмпирического распределения от нормального используют различные характеристики, к числу которых относятся асимметрия и эксцесс.Асимметрия эмпирического распределения определяется равенством as=m3/ Эксцесс эмпирического распределения определяется равенством: ek=m4/
|
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 668. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
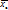 и
и  , например, по методу произведений;
, например, по методу произведений; (выравнивающие частоты) теоретической кривой по формуле
(выравнивающие частоты) теоретической кривой по формуле 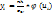 , где n – сумма наблюдаемых частот, h – разность между двумя соседними вариантами:
, где n – сумма наблюдаемых частот, h – разность между двумя соседними вариантами: 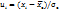 и
и 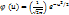 ;
;