
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Сравнение наблюдаемой относительной частоты с гипотетической вероятностью появления событияПусть по достаточно большому числу п независимых испытаний; в каждом из которых вероятность р появления события постоянна, но неизвестна, найдена относительная частота т/п. Пусть имеются основания предполагать, что неизвестная вероятность равна гипотетическому значению р0. Требуется при заданном уровне значимости а проверить нулевую гипотезу, состоящую в том, что неизвестная вероятность р равна гипотетической вероятности р0. Поскольку вероятность оценивается по относительной частоте, рассматриваемую задачу можно сформулировать и так: требуется установить, значимо или незначимо различаются наблюдаемая относительная частота и гипотетическая вероятность. В качестве критерия проверки нулевой гипотезы примем случайную величину
где Величина V при справедливости нулевой гипотезы распределена приближенно нормально с параметрами Пояснение. Доказано (теорема Лапласа), что при достаточно больших значениях n относительная частота имеет приближенно нормальное распределение с математическим ожиданием р и средним квадратическим отклонением
При справедливости нулевой гипотезы, т. е. при р = р0, Замечание1: Далее набл-мая частота обозн-ся ч/з М/п правила проверки нулевой гипотезы: Правило 1. Для того чтобы при заданном уровне значимости проверить нулевую гипотезу H0:р = р0 о равенстве неизвестной вероятности гипотетической вероятности при конкурирующей гипотезе  и по таблице функции Лапласа найти критическую точку ыкр по равенству Если |Uнабл|<uкр—нет оснований отвергнуть нулевую гипотезу Если | Uнабл 1>uкр—нулевую гипотезу отвергают. Правило 2. При конкурирующей гипотезе H1:р>р0 находят критическую точку правосторонней критической области по равенству Ф(uкр) = (1—2а)/2. Если |Uнабл|<uкр—нет оснований отвергнуть нулевую гипотезу. Если|Uнабл|>uкр—нулевую гипотезу отвергают. Правило 3. При конкурирующей гипотезе H1:р< р0 находят критическую точку uкр по правилу 2, а затем полагают границу левосторонней критической области Uкр =-uкр Если|Uнабл|<uкр—нет оснований отвергнуть нулевую гипотезу. Если |Uнабл|>uкр—нулевую гипотезу отвергают. Замечание 2. Удовлетворительные результаты обеспечивает выполнение неравенства np0q0>9 |
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 445. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


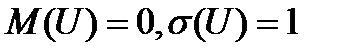 .
.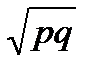 /n. Нормируя относительную частоту (вычитая математическое ожидание и деля на среднее квадратическое отклонение), получим
/n. Нормируя относительную частоту (вычитая математическое ожидание и деля на среднее квадратическое отклонение), получим 'причем М(U) = 0,
'причем М(U) = 0,  .
.
 , надо вычислить наблюдаемое значение критерия:
, надо вычислить наблюдаемое значение критерия: 
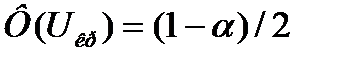 .
.