
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Сравнение нескольких дисперсий нормальных генеральных совокупностей по выборкам различного объема. Критерий БартлеттаПусть генеральные совокупности Х1г Х2, .... распределены нормально Из этих совокупностей извлечены независимые выборки, вообще говоря, различных объемов п1, п2, … . По выборкам найдены исправленные выборочные дисперсии Требуется по исправленным выборочным дисперсиям при заданном уровне значимости а проверить нулевую гипотезу, состоящую в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой:Н0=D(X1)=D(X2)=D(Xi). Другими словами, требуется установить, значимо или незначимо различаются исправленные выборочные дисперсии. Рассматриваемую здесь гипотезу о равенстве нескольких дисперсий называют гипотезой об однородности дисперсий. Заметим, что числом степеней свободы дисперсии Обозначим через В качестве критерия проверки нулевой гипотезы об однородности дисперсий примем критерий Бартлетта — случайную величину: В = V/С. Бартлетт установил, что случайная величина Впри условии справедливости нулевой гипотезы распределена приближенно как |
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 412. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
.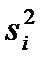 называют число
называют число 
 , т. е. число, на единицу меньшее объема выборки по которой вычислена дисперсия.
, т. е. число, на единицу меньшее объема выборки по которой вычислена дисперсия.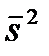 среднюю арифметическую исправленных дисперсий, взвешенную по числам степеней свободы:
среднюю арифметическую исправленных дисперсий, взвешенную по числам степеней свободы:  , где
, где  .
. с l—1 степенями свободы, если все кi> 2. Учитывая, что ki=ni-l, заключаем, что ni- 1 > 2, или пi> 3, т. е. объем каждой из выборок должен быть не меньше 4.
с l—1 степенями свободы, если все кi> 2. Учитывая, что ki=ni-l, заключаем, что ni- 1 > 2, или пi> 3, т. е. объем каждой из выборок должен быть не меньше 4.