
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Олимпиадные задачи.Основы теории чисел:простые числа, алгоритм ЭвклидаЦелые числа включают в себя множество отрицательных чисел,положительных(натуральных) и число ноль Наибольший общий делитель (НОД) – это число, которое делит без остатка два числа и делится само без остатка на любой другой делитель данных двух чисел. Проще говоря, это самое большое число, на которое можно без остатка разделить два числа, для которых ищется НОД. Наибольший общий делитель чисел a, b можно найти с помощью алгоритма Евклида, который состоит в следующем. Пусть b>0. Разделим a на b, тогда по теореме о делении с остатком: a = bq1 + r1. Если r1 = 0, то НОД(a, b) = b. Если r1 ¹ 0, то разделим b с остатком на r1: b = r1q2 + r2. Если r2 = 0, то процесс деления закончим, а если r2 ¹ 0, то разделим r1 с остатком на r2: r1 = r2q3 + r3. Продолжая далее таким же образом, мы закончим процесс деления как только получится остаток равный 0. Заметим, что такой остаток обязательно получится. В самом деле, остаток всегда меньше делителя, поэтому b > r1 > r2 > r3 > . . . и число получаемых остатков не превосходит b. Итак, в результате указанного алгоритма получим, что:
Тогда на основании свойств 20 и 10 : НОД(a, b) = НОД(b, r1) = НОД(r1, r2) = . . . = НОД(rn-1,rn) = rn. Следовательно, наибольший общий делитель чисел a и b совпадает с последним ненулевым остатком rn в алгоритме Евклида для чисел a и b.
Олимпиадные задачи, решаемые с использованием принципа Дирихле "Если в n клетках сидит n+1 или больше зайцев, то найдётся клетка, в которой сидят по крайней мере два зайца". В ряде задач применяют следующее обобщение принципа Дирихле. 
ФОРМУЛИРОВКА 3. "Если nk+1 зайцев размещены в n клетках, то найдутся k+1 зайцев, которые посажены в одну клетку (n, k - натуральные числа)". Принцип Дирихле в теории чисел
Следующую теорему часто используют в школьном курсе алгебры, но доказательство не рассматривают. Его очень просто получить с помощью принципа Дирихле.
ТЕОРЕМА 1. Пусть p, q - натуральные числа, p < q. Если обыкновенную дробь p/q обратить в десятичную, то получится либо конечная, либо бесконечная периодическая десятичная дробь, причём длина периода не превосходит q-1. ТЕОРЕМА 2. Любой многочлен с целыми коэффициентами (отличный от константы) при некотором натуральном значении аргумента принимает значение, представляющее собой составное число.
Комбинаторные задачи, приемы и методы их решения. Выбором объектов и расположением их в том или ином порядке приходится заниматься чуть ли не во всех областях человеческой деятельности, например, конструктору, который разрабатывает новую модель механизма, ученому-агроному, который планирует распределение сельскохозяйственных культур на нескольких полях, химику, который изучает строение молекул. С аналогичными задачами, получившими название комбинаторных, люди столкнулись в глубокой древности, а раздел математики занимающийся этими задачами получил название комбинаторика. Что же такое комбинаторика? Комбинаторика – это раздел математики, в котором изучают, сколько комбинаций, подчиненных тем или иным условиям, можно составить из данных объектов Комбинаторные задачи обладают общей особой приметой. Этой приметой является вопрос задачи, который всегда можно сформулировать так, что он будет начинаться словами: «Сколько … ?», «Сколькими способами …?». Комбинаторные задачи различаются по подходам к решению. Рассмотрим некоторые основные комбинаторные идеи, лежащие в основе решения некоторых из них. правило произведения: Пусть нам даны k множеств по n1, n2, n3, n4,... ,nk элементов каждое, и нам нужно произвести выбор по одному в каждом из множеств, тогда число возможных способов находим так: N = n1 n2 n3 n4 ...nk. Обобщение: на каждое из m мест может быть поставлен элемент n – элементного множества. Тогда количество способов расположения элементов можно найти по формуле mn. Перестановкой из n элементов называют упорядоченный набор этих элементов. Обозначают Pn. Размещением из n элементов по k называется упорядоченное подмножество из n элементов множества, имеющего k элементов. Обозначается Akn Cочетанием из n элементов по k называется неупорядоченное подмножество из n элементов множества, имеющего k элементов. Обозначается Ckn.
Диафантовы уравнения ДИОФАНТОВЫ УРАВНЕНИЯ - алгебраические уравнения или системы алгебраических уравнений, решения которых отыскиваются в целых или рациональных числах. Обычно предполагается, что Д. у. имеют число неизвестных, превосходящее число уравнений, в связи с чем они называются также неопределенными уравнениями. Решение уравнений в целых числах является одной из древнейших математических задач. Уже в начале 2-го тысячелетия до н. э. вавилоняне умели решать системы таких уравнений с двумя неизвестными. Наибольшего расцвета эта область математики достигла в Древней Греции. Уравнения названы в честь греческого математика Диофанта, который жил в третьем веке нашей эры. Эти уравнения имеют простую структуру в виде равенства нулю многочлена от многих неизвестных. Диофантовыми уравнениями называются уравнения вида При исследовании диофантовых уравнений обычно ставятся следующие вопросы: 1. имеет ли уравнение целочисленные решения; 2. конечно или бесконечно множество его целочисленных решений; 3. решить уравнение на множестве целых чисел, т. е. найти все его целочисленные решения; 4. решить уравнение на множестве целых положительных чисел; 5. решить уравнение на множестве рациональных чисел. |
||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 273. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , где
, где 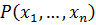 - многочлен с целыми коэффициентами.
- многочлен с целыми коэффициентами.