
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Обобщенные приемы познавательной деятельности процесса поиска решения задачДинамизацию геометрических объектов можно использовать двояко: как цель (при этом формулируются динамические задачи), как средство (при этом любая нединамическая задача проходит через динамику, отвлекаясь потом от последней). Для решения задач обоих классов используются достаточно обобщенные приемы познавательной деятельности учащихся. Эти приемы, носят достаточно обобщенный характер и могут служить ориентировочной основой действий учащихся в ходе решения различных типов задач. Это задачи на: 1. Опровержение ложных формул или других ложных утверждений. 2. На отыскание неизвестных элементов и отношений между ними. 3. Задачи на доказательство. 4. Задачи на построение. 5. Задачи на определенность геометрической фигуры. 6. Задачи на отыскание геометрического места точек. 7. Задачи на установление функциональных зависимостей.
4. Рассуждение по аналогии имеет следующую общую схему: А обладает свойствами А, В, С, Д, В обладает свойствами А, В, С, Вероятно (возможно) В обладает и свойством Д. Как видим, заключение по аналогии является лишь вероятным (правдоподобным), а не достоверным. Поэтому аналогия, как правило, не является доказательным рассуждением, т. е. рассуждением, которое может служить доказательством. ("Как правило" потому, что имеется исключение, связанное с особым видом аналогии, о котором речь пойдет дальше.) Однако в обучении, как, впрочем, и в науке, аналогия часто полезна тем, что она наводит нас на догадки, т. е. служит эвристическим методом. В обучении же математике не менее важно, чем учить доказывать, это учить догадываться, что именно подлежит доказательству и как найти это доказательство.  Сфера - пространственный аналог окружности. Эти две фигуры определяются как множества точек плоскости и пространства соответственно, характеризуемые одним и тем же свойством: {X || OX| = r} (множество всех точек плоскости (пространства), расстояние которых от данной точки О равно данному числу r). Это наводит на догадку, что сфера обладает некоторыми свойствами, аналогичными свойствам окружности.
Обобщение - это мысленное выделение, фиксирование каких-нибудь общих существенных свойств, принадлежащих только данному классу предметов или отношений. Под обобщением понимают также переход от единичного к общему, от менее общего к более общему. Под конкретизацией понимают обратный переход - от более общего к менее общему, от общего к единичному. Уточним переход от единичного к общему, от менее общего к более общему и обратный переход. Класс квадрата включается в более широкий класс прямоугольников (переход от общего к более общему). При этом переходе к более широкому классу происходит сужение характеристики класса, одно из свойств, характеризующих класс квадратов (равенство всех сторон), опускается. если к содержанию понятия "прямоугольник" (к множеству свойств, характеризующих класс прямоугольников) добавить новое свойство (равенство всех сторон), мы получим содержание понятия "квадрат" (множество свойств, характеризующих класс квадратов).
Метод математической индукции Пусть мы имеем бесконечную последовательность утверждений P1, P2, ..., Pn, ..., занумерованных натуральными числами, причём: — утверждение P1 истинно; — если некоторое утверждение Pk истинно, то следующее утверждение Pk+1 тоже истинно. Тогда принцип математической индукции утверждает, что все утверждения последовательности истинны. Другими словами принцип математической индукции можно сформулировать так: если в очереди первой стоит женщина, и за каждой женщиной стоит женщина, то все в очереди – женщины. Способ рассуждений, основанный на принципе математической индукции называется методом математической индукции. Для решения задач методом математической индукции необходимо: 1) сформулировать утверждение задачи в виде последовательности утверждений P1, P2, ..., Pn, ... 2) доказать, что утверждение P1 истинно (этот этап называется базой индукции); 3) доказать, что если утверждение Pn истинно при некотором n = k, то оно истинно и при n = k + 1 (этот этап называется шагом индукции).
Функция Функция— математическое понятие, отражающее связь между элементами множеств. Можно сказать, что функция это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений). Свойства: область определения; область значения; четность; возрастание, убывание; периодичность. Четность Функция f (x) называется четной, если для любого График четной функции на всей области определения симметричен относительно оси OY. Примерами четных функций могут служить y = cos x, y = |x|, y = x2 + |x|. Функция f (x) называется нечетной, если для любого Иными словами функция называется нечетной, если ее график на всей области определения симметричен относительно начала координат. Примерами нечетных функций являются y = sin x, y = x3. Монотонность Функция f (x) называется возрастающей на промежутке D, если для любых чисел x1 и x2 из промежутка D таких, что x1 < x2, выполняется неравенство f (x1) < f (x2). Функция f (x) называется убывающей на промежутке D, если для любых чисел x1 и x2 из промежутка D таких, что x1 < x2, выполняется неравенство f (x1) > f (x2). Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке. Ограниченность функций Если для любого (xÎD, x ≠ a) выполняется неравенство f (x) ≤ f (a) , aÎD то точка a называется точкой наибольшего значения функции на множестве D:
Если для любого xÎD выполняется неравенство f (x) > f (b) bÎD то точка b называется точкой наименьшего значения функции на множестве D.
Если существует число C такое, что для любого xÎD выполняется неравенство f (x) ≤ C, то функция f называется ограниченной сверху на множестве D. Если существует число c такое, что для любого xÎD выполняется неравенство f (x) ≥ c, то функция f называется ограниченной снизу на множестве D. Функция, ограниченная и сверху, и снизу, называется ограниченной на множестве D. Геометрически ограниченность функции f на множестве D означает, что график функции y = f (x), xÎD лежит в полосе c ≤ y ≤ C. Если функция не является ограниченной на множестве, то говорят, что она не ограничена. Примером функции, ограниченной снизу на всей числовой оси, является функция y = x2. Примером функции, ограниченной сверху на множестве (–∞; 0) является функция y = Примером функции, ограниченной на всей числовой оси, является функция y = sin x. |
||||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 215. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
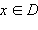 выполняются равенства:
выполняются равенства:  ,
,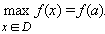
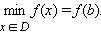
 .
.