
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Координаты вектора в базисеЭлементы a1, ... ,aпполя Р в равенстве а = u1a1+ ... + ипaп , в котором Для любого фиксированного базиса линейного пространства Lкаждому вектору однозначно ставится в соответствие столбец его координат. В пространстве L кроме базиса Столбцы матрицы Система векторв Формула преобразования координат векторов в различных базисах В n-мерном линейном пространстве L над полем Р рассмотрим произвольный вектор a. Пусть Таким образом, выполняются следующие соотношения:  Изоморфизм линейных пространств одинаковой размерности Любое линейное пространство размерности n>0 над полем Р изоморфно пространству Р(n). Отсюда становится ясно, что для изоморфизма двух произвольных конечномерных линейных пространств над одним и тем же полем необходимо и достаточно, чтобы они имели одну и ту же размерность. Скалярное произведение векторов Скалярным умножениемвекторов пространства Lнад полем действительных чисел R называется бинарная операция, по которой каждой паре α, β векторов из Lставится в соответствие определенное число из R, обозначаемое в виде (α, β). Причем, для любых векторов α, β, γ из Lи любого числа rÎR должны выполняться следующие соотношения: 1) (α, β) = (β,α); 2) (α+β, γ) = (α, γ) +(β, γ); 3) (αr, β) = r(α, β) 4) (α, α) > 0, если α ≠ θ. При этом число (α, β) называется скалярным произведениемвекторов α, β. Линейное пространство L над полем действительных чисел R с определенной операцией скалярного умножения векторов называется евклидовым пространством. Рассмотрим линейное n-мерное пространство столбцов R(n) над полем R. Для элементов этого пространстваскалярное умножение может быть определено следующим образом: Определенное скалярное произведение часто называют каноническим.Скалярное произведение векторов-функций может быть определено следующей формулой: Нормированные пространства Для произвольного линейного пространства L над полем действительных чисел R вместо термина «длина» используется термин «норма», а для обозначения нормы элемента aÎL используется обозначение |a|.Для нормы любых векторов α, βÎLи любого числа rÎR должны выполняться следующие соотношения: 1) 2) 3) Последнее, третье свойство носит название аксиомы треугольника. Оно соответствует тому факту, что длина любой стороны треугольника меньше суммы длин двух других его сторон. Все три, приведенные выше свойства называют аксиомами нормы, а линейное пространство над полем действительных чисел R с заданной нормой, называют нормированным. Норма вектора a евклидова пространства, обозначаемая
Метрические пространства Если в произвольном линейном пространстве L над полем действительных чисел R для любых двух векторов α,bÎL определена числовая функция ρ(α, β)ÎR, обладающая следующими свойствами: 1) ρ(α, β)> 0 при α ≠ β; ρ(α, α) = 0 2) ρ(α, β) = ρ(β, α); 3) ρ(α, β) + ρ(β, γ) ≥ ρ(α, γ), γÎL , то ρ(α,β) называется расстоянием или метрикой, а пространство L называется метрическим пространством. Приведенные выше три свойства называются аксиомами метрики. Для установления справедливости третьей аксиомы метрики также было использовано неравенства Коши-Буняковского: Доказательство:если α = θ, то | θ |·|β | = 0·|β | =0 и |(θ, β)| = 0, следовательно неравенство выполняется. Будем теперь считать α≠θ. По свойствам скалярного произведения (αr + b, αr +b) (αr + b, αr +b) = r2(α, α) + 2r(α, b) + (b,b), при
Отсюда, в силу того, что левая и правая части последнего неравенства неотрицательны, получаем: Полученное неравенство при α ≠ θ, β ≠ θ может быть записано следующим образом: Отсюда следует возможность введения угла jÎ[0,p] между ненулевыми векторами α и β евклидова пространства, который определяется соотношением: |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 224. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
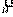 = (u1,... ,ип) базис n-мерного пространства L над полем Р называются координатами вектора а в базисе
= (u1,... ,ип) базис n-мерного пространства L над полем Р называются координатами вектора а в базисе  называется столбцом координатвектора а в базисе
называется столбцом координатвектора а в базисе 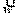 = (w1,..., wn). Каждый вектор этого нового базиса может быть линейно выражен через вектора базиса
= (w1,..., wn). Каждый вектор этого нового базиса может быть линейно выражен через вектора базиса 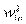 , . . . , wn=
, . . . , wn=  , которая в свою очередь может быть записана в матричном виде следующим образом:
, которая в свою очередь может быть записана в матричном виде следующим образом:  .
. являются столбцами координат векторов базиса
являются столбцами координат векторов базиса  также будет базисом линейного пространства L тогда и только тогда, когда В — невырожденная матрица. Матрица перехода от базиса
также будет базисом линейного пространства L тогда и только тогда, когда В — невырожденная матрица. Матрица перехода от базиса  Dявляется обратной для матрицы B перехода от базиса
Dявляется обратной для матрицы B перехода от базиса  два базиса пространства L, и
два базиса пространства L, и  ,
,  — столбцы координат вектора а соответственно в базисах
— столбцы координат вектора а соответственно в базисах  ,
,  . Воспользуемся полученной ранее матричной зависимостью векторов двух рассматриваемых базисов
. Воспользуемся полученной ранее матричной зависимостью векторов двух рассматриваемых базисов  и получим следующее выражение:
и получим следующее выражение:  . В силу однозначности выражаемости вектора а через базис
. В силу однозначности выражаемости вектора а через базис 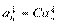 .
. .
. .
. ;
;

 , может быть определена как квадратный арифметический корень из скалярного произведения вектора a на самого себя:
, может быть определена как квадратный арифметический корень из скалярного произведения вектора a на самого себя:  .
. .
.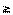 0 (при любом rÎR) и
0 (при любом rÎR) и получаем:
получаем: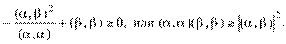
 и далее
и далее  . Что и требовалось доказать.|
. Что и требовалось доказать.| .
. .
.