
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Сравнения целых чисел и их свойстваПусть m – некоторое фиксированное натуральное число. Если любые два целых числа а, b при делении на m дают одинаковые остатки, то говорят, что они сравнимы по модулю m, (число m называют модулем). Обозначается: Пусть имеются произвольные целые числа 1) Число а сравнимо само с собой: 2) Если число a сравнимо с числом b, то и число b сравнимо с a: 3) Если число a сравнимо с числом b и b сравнимо с числом с, то a сравнимо с числом с: 4) Если число a сравнимо с числом b, то m нацело делит разность (a – b): 5) Если имеют места сравнения: 6) Если имеет место сравнение 7) Если имеет место сравнение Классы вычетов по модулю m [r]m- класс всех чисел, которые при делении на m дают в остатке r. Классы [0]m, [l]m, [2]m, …, [m- 1]m называются классами вычетов, а их элементы — вычетами по модулю m. Числа из одного класса сравнимы по модулю m, числа же из разных классов несравнимы друг с другом по модулю m: aºb(modm)Û[а]mº [b]m. Полной системой вычетов по модулю m называется совокупность чисел, взятых по одному из каждого класса вычетов по модулю m. Множество чисел 0, 1,…, m-1 будет являться полной системы вычетов по модулю m. Этим получена так называемая полная система наименьших неотрицательных вычетов. Для полных систем вычетов имеет место следующее свойство: Если a1, a2, …, amесть полная система вычетов по модулю m, число а взаимно простое cm и b — любое целое число, тогда последовательность чиселaa1 + b, aa2 + b, …, aam + b - также есть полная система вычетов по модулю m. Если в классе вычетов по модулю m есть одно число, взаимно простое с m, то в нем все числа взаимно просты с m.  Сравнимость по модулю целых чисел a и b влечет за собой равенство наибольшего общего делителя чисел a и m c наибольшим общим делителем чисел b и m. а Класс вычетов по модулю m, состоящий из чисел, взаимно простых с m, называется классом, взаимно простым с модулем m.Совокупность чисел, взятых по одному из всех классов, взаимно простых с модулем m, называется приведенной системой вычетов по модулю m. Функция Эйлера j(m) Количество чисел в приведенной системе вычетов по модулю m(или количество классов, взаимно простых с модулем m), определяет функцию Эйлера j(m), сопоставляющую числу m число j(m). Значение этой функции j(m) равно количеству натуральных чисел, не превосходящих m и взаимно простых с m. j(mn) = j(m)j(n). Это так называемое свойство мультипликативности функции Эйлера. Из арифметики известен тот факт (основная теорема арифметики), что любое натуральное число единственным образом представимо в виде произведения взаимно простых с ним чисел. Такое представление называется каноническим разложением числа на простые множители. Если число m имеет каноническое разложение Рассмотрим приведенную систему вычетов по модулю m, содержащую Справедливо следующее важное утверждение: набор чисел aa1,,aa2,...,aaj(m) , получающихся умножением приведенной системы вычетов по модулю m на число взаимно простое с модулем m также является приведенной системой вычетов по этому модулю. |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 247. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
. . Свойства:
. Свойства: , (свойство рефлексивности).
, (свойство рефлексивности). , (свойство симметрии).
, (свойство симметрии). , (свойство транзитивности).
, (свойство транзитивности). при некотором
при некотором  .
. , то их можно почленно складывать, вычитать и перемножать:
, то их можно почленно складывать, вычитать и перемножать:  .
. и dесть общий делитель чисел а, b, m, то справедливо и сравнение
и dесть общий делитель чисел а, b, m, то справедливо и сравнение  ,
, .
. b(modm) Þ НОД(а, m) = НОД(b, m).
b(modm) Þ НОД(а, m) = НОД(b, m). , то
, то 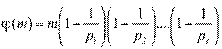
 элементов: а1,a2,...,аj(m). Пусть, число а взаимно просто с m.
элементов: а1,a2,...,аj(m). Пусть, число а взаимно просто с m.