
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Системы однородных линейных уравненийОднородной системой линейных уравнений называется линейная система с нулевым вектором свободных членов. В матричной форме она имеет вид: Если задана произвольная система линейных уравнений Любое решение этой системы может быть получено приданием конкретных значений свободным переменным xr+1,...,хп и однозначным нахождением по правилу Крамера соответствующих значений переменных x1,...,хr. Так для набора значений свободных переменных Аналогично для наборов значений свободных переменных Эти решения образуют так называемую фундаментальную систему решений однородной системы. Все остальные решения однородной системы являются их линейными комбинациями. Структура решений совместных систем линейных уравнений Пусть имеется совместная система линейных уравнений, записанная в матричном виде: В случае, когда решение единственно, оно находится по правилу Крамера и записывается в виде вектора столбца  Рассмотрим теперь однородную систему линейных уравнений Теперь возвращаясь к исходной системе Действительно, пусть Таким образом, мы пришли к общепринятой системе записи общего решения исходной системы линейных уравнений |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 177. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
. , то ассоциированной с ней системой однородных линейных уравнений называют систему уравнений, полученную заменой всех свободных членов bi, (i= 1,..., т) на нули. Очевидно, что однородная система всегда имеет решение, состоящее из всех нулей, то есть такая система всегда совместна.
, то ассоциированной с ней системой однородных линейных уравнений называют систему уравнений, полученную заменой всех свободных членов bi, (i= 1,..., т) на нули. Очевидно, что однородная система всегда имеет решение, состоящее из всех нулей, то есть такая система всегда совместна.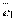 = (1,0,..., 0) получим набор значений
= (1,0,..., 0) получим набор значений  . Объединяя эти наборы, получаем решение однородной системы:
. Объединяя эти наборы, получаем решение однородной системы:  , которые совместно дают решение однородной системы.
, которые совместно дают решение однородной системы. = (0,1,..., 0), ...,
= (0,1,..., 0), ...,  = (0,0,..., 1) могут быть найдены наборы значений переменных x1,...,хr:
= (0,0,..., 1) могут быть найдены наборы значений переменных x1,...,хr:  . Проводя соответствующие объединения, найдем следующие решения однородной системы уравнений:
. Проводя соответствующие объединения, найдем следующие решения однородной системы уравнений:  .
. .
. . Подстановка этого вектора в исходную систему уравнений, записанную в виде матричного соотношения, обращает его в матричное тождество:
. Подстановка этого вектора в исходную систему уравнений, записанную в виде матричного соотношения, обращает его в матричное тождество: 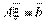 .
. , ассоциированную с исходной системой
, ассоциированную с исходной системой  есть решения однородной системы
есть решения однородной системы  также является ее решением при любых с1, с2ÎR. Действительно, из того что
также является ее решением при любых с1, с2ÎR. Действительно, из того что  и
и  . Подставляя в однородную систему
. Подставляя в однородную систему  Следовательно, любая линейная комбинация решений однородной системы линейных уравнений также является ее решением.
Следовательно, любая линейная комбинация решений однородной системы линейных уравнений также является ее решением.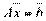 , можно утверждать, что множество
, можно утверждать, что множество  всех решений этой системы может быть записано в виде
всех решений этой системы может быть записано в виде  , где
, где  есть множество всех решений однородной системы
есть множество всех решений однородной системы  - любое фиксированное решение исходной системы уравнений
- любое фиксированное решение исходной системы уравнений  , то
, то  , а
, а  ).
). , тогда
, тогда  и
и  . С другой стороны, если
. С другой стороны, если  решение исходной системы (
решение исходной системы (  ), то оно может быть представлено в виде
), то оно может быть представлено в виде  .
. , где
, где  — любое фиксированное решение исходной системы, с1,..., cп-r— любые действительные числа, а
— любое фиксированное решение исходной системы, с1,..., cп-r— любые действительные числа, а  фундаментальная система решений ассоциированной однородной системы уравнений
фундаментальная система решений ассоциированной однородной системы уравнений