
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Бинарные отношения. Отношения эквивалентностиБинарным отношением на множестве А называется любое подмножество множества из пар чисел (a, b), где Если r- любое отношение на множестве А, то для произвольного элемента а из А можно определить подмножество элементов, находящихся с ним в отношении rи обозначить это подмножество через[а]r={b [а]>={b Отношением эквивалентности на непустом множестве А называется бинарное отношение r,удовлетворяющее следующим свойствам: для любого для любых a, b для любых a, b, cÎАиз аrbиbrа следует, аrc(транзитивность). На множестве всевозможных прямых линий плоскости отношение параллельности двух прямых является отношением эквивалентности. Если rесть отношение эквивалентности, то элементы, связанные отношением r, называются эквивалентными, а подмножества [а]r- классами эквивалентности. Все элементы одного класса эквивалентны между собой, а любые элементы из разных классов - не эквивалентны. Полугруппы и группы Непустое множество Gс одной бинарной алгебраической операцией * называется группоидоми обозначается в виде (G, *). В случае, когда операция * ассоциативна, группоид(G, *) называется полугруппой. Группоид (G, *) называется группой, если выполняются три условия: операция * ассоциативна, т. е. (G, *) - полугруппа; в Gесть нейтральный элемент e, такой, что a* e = e *a=a для любого aÎG; для любого элемента aÎGв Gсуществует обратный к нему элемент a¢, такой элемент, что a*a¢=a¢*a=e. В случае, когда операция * коммутативна, группа называется коммутативной, или абелевой. (Абель Н. X. (1802 - 1829) – норвежский математик).  Произвольная группа G может записываться в мультипликативной либо в аддитивной форме. В первом случае (мультипликативном) операция в группоиде называется умножение и обозначается обычным знаком умножения; нейтральный элемент e называется единицей или единичным элементом и обозначается 1, а элемент a¢ , обратный к элементу a,обозначается a-1. В аддитивном случае операция в группоиде Gназывается сложение и обозначается +; нейтральный элемент eназывается нулем или нулевым элементом и обозначается 0, а элемент a¢ называется противоположным к a и обозначается «-a». |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 173. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
.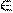 А: arb}. Для рассматриваемого примера бинарного отношения >будем иметь:
А: arb}. Для рассматриваемого примера бинарного отношения >будем иметь: аrа, ( рефлексивность);
аrа, ( рефлексивность); из аrbследует brа, (симметричность);
из аrbследует brа, (симметричность);