
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Применение матриц к решению систем линейных уравнений. Матричная запись произвольной системы линейных уравненийПусть имеется произвольная система из m линейных уравнений с n неизвестными:
Применим матричные обозначения:
Используя введенные обозначения и свойства матричных операций исходную систему линейных уравнений можно записать в матричной форме: Условие совместности произвольной системы линейных уравнений Система линейных уравнений имеет решение (совместна) тогда и только тогда, когда ранг ее матрицы равен рангу расширенной матрицы системы, то есть в наших обозначениях rangА = rang Это утверждение называется теоремой Кронекера-Капелли. Системы линейных уравнений имеющие единственное решение и правило нахождения этого решения Система линейных уравнений имеет единственное решение тогда и только тогда, когда ранги ее матрицы и расширенной матриц совпадают и равны числу неизвестных, т. е. В частном случае, когда количество уравнений равно количеству неизвестных, то есть т = n и матрица системы уравнений А невырожденная. Значит определитель |А| = Δ системы уравнений не равен нулю. В этом случае имеет место, так называемое правило Крамера, по которому исходная система линейных уравнений имеет единственное решение, которое находится по формулам Крамера Нахождение решений совместных систем линейных уравнений общего вида  Пусть имеется система линейных уравнений, для которой выполняется условие: По определению ранга в матрице А существуетневырожденная квадратная подматрица порядка r. Не теряя общности, для простоты рассуждений пусть это будет подматрица
Члены с первыми r неизвестными оставим в левых частях уравнений системы. Остальные неизвестные будем считать пока некоторыми параметрами и перенесем члены, их содержащие, в правые части уравнений. Теперь, преобразованную описанным образом систему можно рассматривать, как систему r уравнений с r неизвестными с определителем, отличным от нуля. К решению этой системы можно применить формулы Крамера, по которым неизвестные х1,... ,хrвыражаются через остальные неизвестные xr+1,... ,хп. Придавая этим неизвестным xr+1,... ,хпвсевозможныепроизвольные значения, могут быть получены все решения исходной системы. |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 176. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


 — матрица коэффициентов при неизвестных в уравнениях системы, где i – номер уравнения, а j – номер неизвестного;
— матрица коэффициентов при неизвестных в уравнениях системы, где i – номер уравнения, а j – номер неизвестного; – столбец свободных членов (правых частей уравнений системы);
– столбец свободных членов (правых частей уравнений системы); — расширенная матрица системы, матрица коэффициентов и свободных членов;
— расширенная матрица системы, матрица коэффициентов и свободных членов; столбец неизвестных.
столбец неизвестных.
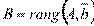 .
. .
. , где Δi, — определитель матрицы Bi, полученной из А заменой ее i-го столбца столбцом свободных членов
, где Δi, — определитель матрицы Bi, полученной из А заменой ее i-го столбца столбцом свободных членов  .
. . То есть ранг матрицы системы равен рангу расширенной матрицы, а количество неизвестных больше ранга.
. То есть ранг матрицы системы равен рангу расширенной матрицы, а количество неизвестных больше ранга. . Тогда последние т - rуравнений являются линейными комбинациями первых r уравнений и не влияют на решения системы. Отсюда следует, что исходная система равносильна системе уравнений:
. Тогда последние т - rуравнений являются линейными комбинациями первых r уравнений и не влияют на решения системы. Отсюда следует, что исходная система равносильна системе уравнений: