
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Ранг матрицы как максимальное количество ее линейно независимых строк или столбцовСтр 1 из 16Следующая ⇒ Определители n-го порядка Определителемквадратной матрицы
Суммирование в приведенной формуле проводится по всем n! перестановкам _(i1,i2,…,in) чисел 1,2,..., n, aI(i1,i2,…,in)есть число инверсий в перестановке (i1,i2,…,in). Свойства определителей n-го порядка Определители n-го порядка обладают свойствами аналогичными, указанным в Лекции 1 для определителей 3-го порядка. 1. Если в матрице А имеются две одинаковые строки (или два одинаковых столбца), то ее определитель равен нулю. 2. Если все элементы какой-либо строки матрицы умножить на число s то и ее определитель умножится на это число s. 3. Если каждый элемент s-й строки матрицы j = 1,..., n, то определитель матрицы А равен сумме определителей матриц А', А", полученных заменой в матрице Аs-й строки соответственно строчками a¢s1, a¢s2,…a¢snи a²s1, a²s2,…, a²sn. 4. Если к какой-либо строке (или столбцу) матрицы прибавить другую ее строку (или столбец), умноженную на любое число, то значение определителя матрицы не изменится. 5. Если в матрице переставить местами какие-либо две строки (или два столбца), то значение определителя измененной матрицы будет отличаться от определителя исходной матрицы только знаком.  6. Определитель транспонированной матрицы АТравен определителю исходной матрицы А, т. е |АТ| = |А|. 7. Пусть А и В квадратные матрицы одной размерности. Тогда определитель произведения этих матриц равен произведению их определителей, то есть: |АВ| = |А||В|. Миноры и алгебраические дополнения Минором матрицы А называется определитель квадратной матрицы, полученной из А удалением некоторого количества ее строк и столбцов. Миноромэлемента aij матрицы А = (aij)nxn называется определитель Mij матрицы, получаемой из А вычеркиванием ее i-й строки и j-ro столбца. Минор элемента aij, умноженный на (-1)i+j, называется алгебраическим дополнением элемента aijи обозначается в виде Aij. Сумма произведений элементов какой-либо строки матрицы
Сумма произведений элементов любой строки матрицы на алгебраические дополнения соответствующих элементов другой строки равна нулю, т. е. . Если вi-й строке матрицы A все элементы, кроме, может быть, элемента aij, равны нулю, то|А| =aijAij. . Матрица А называется блочной, если она может быть записана в следующем виде: Обратная матрица. Матрицей обратной для квадратной матрицы А называется матрица А*,удовлетворяющая условию АА* = А*А = Е, где Е — единичная матрица. Если для матрицы А существует обратная матрица А*, то она единственна. Матрицу, обратную к А, обычнообозначают в виде A-1. Таким образом, обратная матрица A-1может быть определена равенством: АA-1 = A-1A= Е. Для существования матрицы обратной к матрице А необходимо и достаточно чтобы определитель матрицы был отличен от нуля, то есть Действительно в случае существования для матрицы А обратной матрицы A-1, могут быть записаны следующие равенства: АA-1 = A-1A= Е. Отсюда по свойству определителей |А||A-1|= |Е|= 1. Отсюда следует, что |A-1| = |А|-1и обязательно|А| ≠0.
Если определитель матрицы A не равен нулю, то матрица называется невырожденной или неособенной матрицей. В противном случае она называется вырожденной или особенной. Таким образом, для того чтобы матрица А имела обратную необходимо и достаточно чтобы она была невырожденной. Понятие ранга матрицы Любую матрицу, полученную из исходной матрицы А удалением некоторых ее строк и столбцов будем называть ее подматрицей. Наибольший порядок всевозможных невырожденных подматриц данной матрицы А называется рангом матрицы А и обозначается через rangA. Ранг нулевой матрицы равен 0. Преобразования матриц не меняющие их ранг получили название элементарных преобразований. Элементарными преобразованиями матрицы А называются: - умножение любой строки матрицы на отличное от нуля число; - умножение любого столбца матрицы на отличное от нуля число; - прибавление к любой строке матрицы любой другой строки, умноженной на произвольное число; - прибавление к любому столбцу матрицы любого другого столбца, умноженного на произвольное число. - перестановка местами любых двух строк матрицы; - перестановка местами любых двух столбцов матрицы. Для нахождения ранга матриц используется приведение исходной матрицы к матрице, верхняя левая подматрица которой является единичной матрицей некоторого порядка r, а все остальные элементы, не вошедшие в указанную подматрицу, - нулевые.Такие матрицы называются каноническими.. Ранг матрицы как максимальное количество ее линейно независимых строк или столбцов Матрица, состоящая из одного столбца или одной строки, называется вектором. Для обозначения векторов часто используются строчные буквы надчеркнутые сверху. Выражения вида Если имеет место соотношение Если взять некоторое количество равно размерных векторов-столбцов (или векторов-строк) и образовать из них матрицу, то окажется, что ранг этой матрицы будет равен количеству линейно независимых векторов во взятом множестве векторов. Определитель квадратной матрицы равен нулю тогда и только тогда, когда хотя бы одна ее строка (или столбец) является линейной комбинацией остальных. |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 222. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 n-го порядка называется число, равное алгебраической сумме n! членов вида
n-го порядка называется число, равное алгебраической сумме n! членов вида  , где (i1,i2,…,in)— перестановка чисел 1,2,...,п, при этом слагаемое берется со знаком "плюс", если перестановка (i1,i2,…,in) - четная, и со знаком "минус", если она нечетная. Определитель матрицы А обозначается в виде |А|. Определитель любой матрицы порядка nназывается также определителем n-го порядка.
, где (i1,i2,…,in)— перестановка чисел 1,2,...,п, при этом слагаемое берется со знаком "плюс", если перестановка (i1,i2,…,in) - четная, и со знаком "минус", если она нечетная. Определитель матрицы А обозначается в виде |А|. Определитель любой матрицы порядка nназывается также определителем n-го порядка.
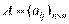 представлен в виде суммы asj = a'sj + a"sj,
представлен в виде суммы asj = a'sj + a"sj, на их алгебраические дополнения равна определителю матрицы А:
на их алгебраические дополнения равна определителю матрицы А:  , i = 1, 2,…… , n.
, i = 1, 2,…… , n. , i ≠ k
, i ≠ k , где B, C, D — матрицы соответственно размеровk×k,k×(n-k),(n-k)×(n-k), а О — нулевая матрица размеров (n-k)×k. Тогда |A| = |B||D|.
, где B, C, D — матрицы соответственно размеровk×k,k×(n-k),(n-k)×(n-k), а О — нулевая матрица размеров (n-k)×k. Тогда |A| = |B||D|.  .
.
 , где
, где 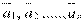 - вектора одинаковой размерности и сi
- вектора одинаковой размерности и сi 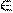 R. (R – множество действительных чисел), называется линейной комбинацией векторов
R. (R – множество действительных чисел), называется линейной комбинацией векторов  .
. , то говорят, что вектор
, то говорят, что вектор  линейно выражается через вектора
линейно выражается через вектора