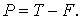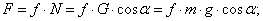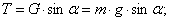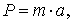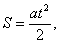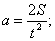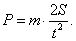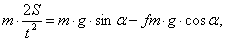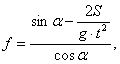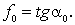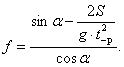Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
А) схема смешанной неуравновешенности; б) расчетная схема
Разложим силы инерции P и Q на параллельные составляющие Р1 и Р2, Q1 и Q2, лежащие в плоскостях уравновешивания и приложенные попарно в точках К1 и К2. Заменим составляющие P1 и Q1 их равнодействующей Ф1, а составляющие P2 и Q2 - равнодействующей Ф2. Силу инерции Ф1, действующую в плоскости уравновешивания 1, можно уравновесить противовесом массы
Аналогично уравновешивается и сила инерции Ф2 (получена от сложения P2 и Q2) в плоскости уравновешивания II:
Таким образом, добавочные грузы (противовесы), массы которых равны Плоскости уравновешивания выбираются из соображений удобства или конструктивно. Величину уравновешивающей силы инерции в каждой из плоскостей уравновешивания можно представить в виде:
Скалярное произведение
где i =1,2 , носит название статического момента уравновешивающей массы или дисбаланса звена. Положение линии действия уравновешивающей силы инерции (положение плоскости дисбаланса) определяется углом Следует заметить, что дисбаланс не зависит от скорости вращения В последнем примере неуравновешенности вала при расположении неуравновешенных масс по рис. 5, а, имеет место две плоскости дисбаланса. Положение этих плоскостей определяется углами
П Р А К Т И Ч Е С К А Я Ч А С Т Ь 
На рис. 6 изображена схема станка, предложенного Б.В.Шитиковым для динамической балансировки роторов. Рама (1) может колебаться вокруг горизонтальной оси О, перпендикулярной оси вращения ротора. Амплитуда А колебаний рамы определяется с помощью максимального (не сбрасывает показаний) индикатора (2). Разгон ротора производится электромотором (3) при нажатии на рукоятку (4). Восстанавливающий момент при колебаниях рамы обеспечивается торсионной пружиной (5). В подшипниках (6) установлен уравновешивающий ротор (7). На валу ротора закреплены два диска (8) и (9) с прорезями для установки уравновешивающих масс. Эти диски моделируют плоскости уравновешивания - I и II . Плоскость уравновешивания II (диск 9) выбрана так, что в ней располагается ось О колебаний рамы 1. Неуравновешенная сила инерции Ф2 , лежащая в этой плоскости не дает момента относительно оси О. Момент относительно осиО создает только неуравновешенная сила инерции Ф1, лежащая в плоскости уравновешивания (I-I) (диск 8). Момент этой силы равен:
где Этот момент вызывает вынужденные колебания рамы (1) вокруг оси О.
Рис. 6. Схема станка для динамической балансировки ротора: Неуравновешенность в плоскости (I-I) (диск 8) представим как статический момент неуравновешенной массы
Задача состоит в определении численного значения, направления и плоскости действия этого статического момента.
Последовательность выполнения работы 1. По уровню проверьте горизонтальность установки рамы (1). 2. Совместите риску диска (8) с нулевым делением нониуса. 3. Электромотором (3) разгоните ротор (7) за резонансные обороты. Отключите электромотор. 4. Измерьте индикатором (2) резонансную амплитуду А1при выбеге ротора (рис. 7). Колебания рамы 1 с амплитудой А1 вызваны имеющим место дисбалансом 5. В любую прорезь диска 8 установите один из грузов массы
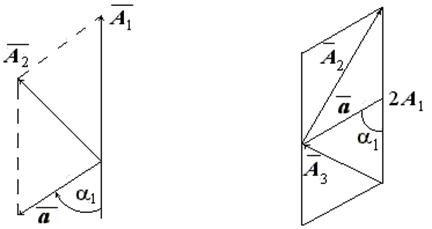
Рис. 7. Резонансная амплитуда при выбеге ротора 6. Повторите операции 3 и 4. Измерьте резонансную амплитуду А2. Амплитуда А2 может быть представлена как геометрическая сумма амплитуд А1 и а (рис. 9):
где а - амплитуда колебаний от установленного груза с массой 7. Груз с массой 8. Повторите операции 3 и 4, измерьте резонансную амплитуду А3. Амплитуда А3 представляется как геометрическая сумма амплитуд А1 и а (рис. 11):
ВНИМАНИЕ! Запомните прорезь, в которой был установлен груз с массой
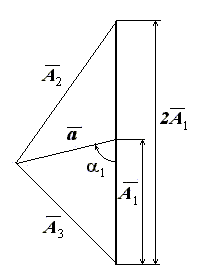
9. Постройте треугольник амплитуд со сторонами 2А1 , А2 , А3 в крупном масштабе (М 100: 1, рис. 13).
Рис. 13. Треугольник амплитуд для определения статического момента
Каждая амплитуда определяется не менее трех раз. Треугольник амплитуд строится по их средним значениям. ВНИМАНИЕ! Расчетным является треугольник амплитуд, построенный на рис.13 (строится только этот треугольник). Построив затем медиану стороны 2А1, найдем в масштабе треугольника амплитуду (-А1) для уравновешивания исходного дисбаланса
и положение осевой плоскости его действия (угол 10. Определите статический момент для уравновешивания исходного дисбаланса:
В соотношении А1 и а - натуральные (не в масштабе) значения амплитуд. Длину отрезка, изображающего амплитуду а, найти из треугольника амплитуд (рис. 13) измерением. Затем умножением на масштаб треугольника перейдите от отрезка к натуре. Исходная неуравновешенность
равны численно, но направлены противоположно. 11. Возьмите допустимую величину уравновешивания массы
12. Измерьте угол Угол 13. Установите уравновешивающую массу 14. Поверните диск 8 на угол ПРИМЕЧАНИЕ. Можно измерить угол 15. Контрольные разгоны. Наибольшая амплитуда после уравновешивания не должна превышать 0,05 мм. Допустимая неуравновешенность (дисбаланс) определяется техническими условиями. При этом задается величина статического момента или амплитуды колебаний. 16. Составьте отчет по прилагаемой форме. ПРИМЕЧАНИЕ. 1. Численное значение и положение плоскости действия исходной неуравновешенности можно определить аналитически по формулам:
Для уравновешивания дисбаланса в плоскости II (плоскость действия силы инерции Ф2) вал необходимо развернуть, установив его так, чтобы плоскость диска 8 прошла через ось О качания рамы, и повторить процесс уравновешивания в плоскости уравновешивания II (диск 9).
Контрольные вопросы
1. Причины и последствия неуравновешенности звеньев. 2. Виды неуравновешенностей. 3. Динамическая неуравновешенность и ее проявление. 4. Динамическая балансировка и ее цель. 5. Принцип работы балансировочного станка Б.В.Шитикова. 6. Порядок выполнения работы по уравновешиванию звена.
Форма отчета
1. Схема установки (по рис. 6)
ПАРАМЕТРЫ ЗАДАВАЕМОГО ДИСБАЛАНСА 2. Масса дополнительного груза - 3. Расстояние дополнительного груза от оси вращения -
4. РЕЗУЛЬТАТЫ ИЗМЕРЕНИЯ АМПЛИТУД (по рис. 13)
5. ТРЕУГОЛЬНИК АМПЛИТУД (по рис.13) 6. Амплитуда колебаний от дополнительного груза -
ПАРАМЕТРЫ БАЛАНСИРОВКИ 7. Масса уравновешивающего груза - 8. Расстояние от центра уравновешивающей массы до оси вращения - 9. Угловая координата уравновешивающей массы - 10. Значение амплитуды после уравновешивания -
Лабораторная работа №31 Определение коэффициента трения скольжения с помощью наклонной плоскости Цель работы: определение коэффициентов трения скольжения для различных материалов контактирующих тел с помощью наклонной плоскости.
Силы трения определяются сопротивлением относительному движению звеньев в кинематических парах. Трение скольжения характеризуется тем, что при относительном движении одни и те же участки одного звена в каждый момент соприкасаются с различными участками другого звена. Согласно закону Кулона
где F – сила трения скольжения; f - коэффициент трения скольжения; N - сила нормального давления. Различают: f – коэффициент кинетического трения (трения движения), f0 – коэффициент статического трения (трения покоя). Коэффициент трения покоя всегда больше коэффициента трения движения:
где
Рис. 1. Тело на наклонной плоскости
Рассмотрим движение тела по наклонной плоскости при Сила, под влиянием которой тело движется, равна:
Составляющие этого уравнения:
После подстановки составляющих
где t – время, за которое тело проходит путь S.
Практическая часть Содержание работы Определение коэффициента трения скольжения покоя и трения скольжения движения для звеньев из различных материалов (сталь – сталь, сталь – дерево, оргстекло – сталь и т. д.). Технология выполнения работы 1. Установить тело (звено) заданного материала на наклонную плоскость. 2. Постепенно увеличивать угол наклона плоскости до момента начала движения тела. Записать угол наклона
3. Поднять плоскость до угла наклона
4. Результаты опытов оформить в виде табл. 1. Таблица 1
5. Оформить отчет.
Контрольные вопросы 1. Дайте определение трению. 2. Какие виды трения вам известны? 3. От каких факторов зависит сила трения при внешнем трении? 4. Какие законы трения вам известны? 5. Что такое трение покоя? 6. Что такое трение скольжения? 7. Как связаны между собой трение покоя и трение скольжения? 8. Что такое коэффициент трения? 9. В каком случае тело находится в равновесии на наклонной плоскости? 10. Другие методы определения коэффициента трения?
Лабораторная работа №32 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 488. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
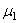 с центром масс на радиусе
с центром масс на радиусе 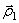 (вектор
(вектор 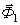 ) исходя при этом из условия:
) исходя при этом из условия: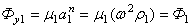 ,
,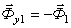 .
.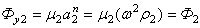 ,
,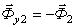 .
.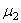 , расположенные в двух произвольно выбранных плоскостях уравновешивания, полностью уравновешивают данную систему сил.
, расположенные в двух произвольно выбранных плоскостях уравновешивания, полностью уравновешивают данную систему сил.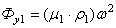 ,
,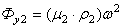 .
.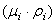 ,
,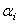 , отсчитываемым от некоторой прямой в плоскости уравновешивания (рис. 5,б; i =1,2).
, отсчитываемым от некоторой прямой в плоскости уравновешивания (рис. 5,б; i =1,2).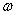 звена.
звена.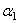 и
и 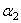 , отсчет которых ведется от некоторой осевой плоскости вала.
, отсчет которых ведется от некоторой осевой плоскости вала.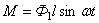 ,
,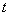 - время.
- время.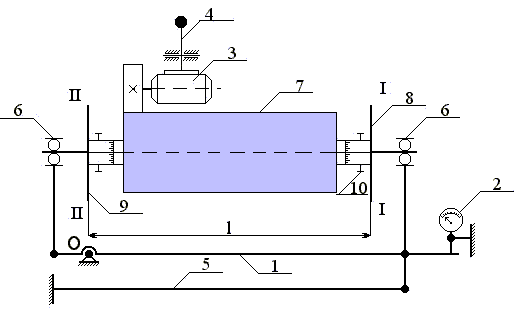
 :
: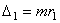 .
.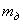 в наборе грузы 10, 20 и 30 г) на выбранном расстоянии
в наборе грузы 10, 20 и 30 г) на выбранном расстоянии 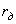 от оси вращения (рис. 8).
от оси вращения (рис. 8).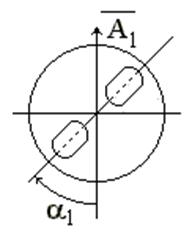
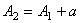 ,
,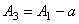 .
.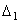 (исходного дисбаланса) в плоскости уравновешивания 1 (диск 8).
(исходного дисбаланса) в плоскости уравновешивания 1 (диск 8).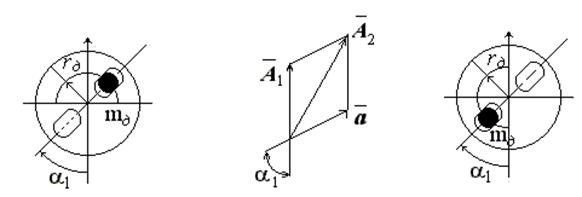
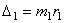
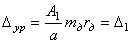 .
.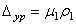 .
.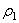 установки этой массы:
установки этой массы: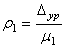 .
.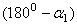 , но тогда уравновешивающую массу
, но тогда уравновешивающую массу 
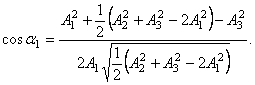
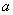 = , (мм)
= , (мм)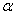 = .
= .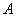 = , (мм).
= , (мм).
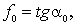
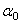 – угол наклона плоскости в момент начала движения тела (звена).
– угол наклона плоскости в момент начала движения тела (звена).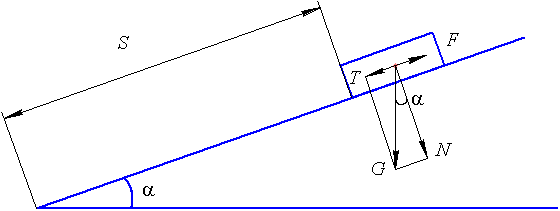
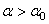 .
.