
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Приводные колеса; 6 - корпус
“сателлитами”, а с Передаточное отношение главной передачи автомобиля через число зубьев колес:
Передаточное отношение самого дифференциала через числа зубьев колес:
Передаточное отношение (3) дифференциала называют внутренним, или еще его называют кинематическим параметром и обозначают буквой Дифференциал, у которого число зубьев
В автомобилестроении главная передача и дифференциал заключены в корпус (6), который называют ведущим мостом автомобиля. Этот мост может быть передним (переднеприводной автомобиль) и задним (заднеприводной автомобиль). Имеют место автомобили с передним и задним ведущими мостами одновременно (вездеходы).
КИНЕМАТИЧЕСКИЙ АНАЛИЗ
Обозначим:
где Для симметричного конического дифференциала формула Виллиса
Знак минус указывает на разноименное вращение полуосей (или полуосевых шестерен, что одно и то же) при остановленном водиле (корпусе) дифференциала. Из формулы (5) следует: 
При движении автомобиля по ровному прямолинейному сухому участку дороги частота
Пусть теперь автомобиль поворачивает, например, налево, не изменяя скорости движения ( При повороте автомобиля сателлиты начинают вращаться с частотой Чем быстрее вращается сателлит (чем больше Передаточное отношение между полуосевой шестерней и сателлитом: - через частоту вращения:
- через число зубьев:
Сопоставляя правые части, находим:
При повороте автомобиля, когда включается в работу дифференциал, приращение частоты вращения полуосевых шестерен будет равно:
Для правой полуоси (поворот налево) это приращение будет со знаком (+), для левой - со знаком (-). Тогда частота вращения полуосей (с учетом вращения (9)):
При этом сумма частот вращения полуосей остается постоянной и равной (6). При одной неподвижной полуоси, например, левой, правая полуось вращается с частотой
при
Знак (-), как уже было отмечено, означает, что если одна из полуосей вращается в одну сторону, то другая полуось вращается в сторону, ей противоположную. При этом частота вращения полуосей одинакова. Если теперь при поднятых ведущих колесах автомобиля остановить коронную шестерню (положить
Отсюда находим частоту вращения сателлита:
Напомним, что дифференциал начинает работать только на поворотах и при движении автомобиля по неровной или скользкой дороге. Отметим также, что частота вращения ведущего колеса автомобиля равна частоте вращения соответствующей полуоси (полуосевой шестерни). Скорость поступательного движения автомобиля Скорость на ободе:
где Поступательная скорость:
СИЛОВОЙ АНАЛИЗ
Дифференциал, кроме обеспечения кинематической связи между коронной шестерней, сателлитами и полуосями, распределяет крутящий момент, получаемый от хвостовика, поровну между полуосями, если не учитывать трение между звеньями дифференциала. Крутящий момент на валу коронной шестерни обозначим
Когда дифференциал вступает в работу и возникает трение между его звеньями, то баланс мощностей может быть представлен в виде соотношения:
где
Мощность трения можно выразить через момент трения
Подставим в формулу (16) значения мощностей в выражении через крутящие моменты:
Так как
то выражение (18) с учетом значений
После преобразований
Сократив на
Аналогичное преобразование дает значение крутящего момента на правой полуоси:
Соотношения (20) и (21) позволяют определить значения крутящих моментов на полуосях при работе дифференциала. Из этих соотношений следует, что момент трения В конических зубчатых дифференциалах момент трения
ОПИСАНИЕ И РАБОТА ЛАБОРАТОРНОЙ УСТАНОВКИ
Рис. 3. Кинематическая схема лабораторной установки: |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 423. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
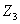 - “полуосевыми шестернями”, т.к. они выполнены непосредственно на концах полуосей (1). Сателлиты и полуосевые шестерни образуют правильное зацепление друг с другом. Они помещены в корпус (2), жестко связанный с коронной шестерней (4). Этот корпус называют “коробкой сателлитов”.
- “полуосевыми шестернями”, т.к. они выполнены непосредственно на концах полуосей (1). Сателлиты и полуосевые шестерни образуют правильное зацепление друг с другом. Они помещены в корпус (2), жестко связанный с коронной шестерней (4). Этот корпус называют “коробкой сателлитов”. (2)
(2) (3)
(3) .
. . (4)
. (4) ,
,  ,
,  - частота вращения (об/мин) левой и правой полуосевых шестерен и коренной шестерни соответственно. Тогда формула Виллиса для конического дифференциала принимает вид:
- частота вращения (об/мин) левой и правой полуосевых шестерен и коренной шестерни соответственно. Тогда формула Виллиса для конического дифференциала принимает вид: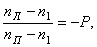
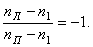 (5)
(5) . (6)
. (6) вращения равна нулю (дифференциал отключен). При таком движении
вращения равна нулю (дифференциал отключен). При таком движении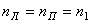 . (7)
. (7) ). Установим соотношения между кинематическими величинами звеньев дифференциала.
). Установим соотношения между кинематическими величинами звеньев дифференциала. . При левом повороте вращение
. При левом повороте вращение 

 (8)
(8) (9)
(9)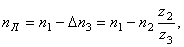
 (10)
(10) , (11)
, (11) из формулы (6):
из формулы (6):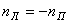 . (12)
. (12) (формула (9)). Вычитая второе соотношение из первого, получим
(формула (9)). Вычитая второе соотношение из первого, получим
 . (13)
. (13) определяется через окружную скорость на ободе ведущего колеса.
определяется через окружную скорость на ободе ведущего колеса. , (14)
, (14) - радиус обода.
- радиус обода. . (15)
. (15)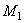 , а соответствующие моменты на полуосях
, а соответствующие моменты на полуосях  и
и  . При одинаковой частоте вращения полуосей и без учета потерь на трение в дифференциале можно записать
. При одинаковой частоте вращения полуосей и без учета потерь на трение в дифференциале можно записать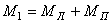 . (16)
. (16) , (17)
, (17)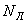 ,
,  - мощность на полуосях соответственно левой и правой;
- мощность на полуосях соответственно левой и правой; - мощность, подводимая к дифференциалу (на валу коронной шестерни);
- мощность, подводимая к дифференциалу (на валу коронной шестерни); - мощность, теряемая на трение в дифференциале.
- мощность, теряемая на трение в дифференциале. (18)
(18) . (19)
. (19) (формула (2)), и
(формула (2)), и (формула (15)),
(формула (15)),
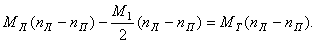
 , получим значение крутящего момента на левой полуоси:
, получим значение крутящего момента на левой полуоси: . (20)
. (20) . (21)
. (21) в дифференциале перераспределяет нагрузку между полуосями, нагружая одну из них и разгружая другую.
в дифференциале перераспределяет нагрузку между полуосями, нагружая одну из них и разгружая другую. (22)
(22)