Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Динамическая балансировка ротора
Цель работы: знакомство с методами уравновешивания вращающихся деталей и узлов, процессом динамической балансировки ротора.
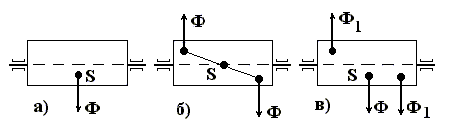
Вращательное движение звеньев является в современной технике одним из доминирующих. При таком движении, как известно, всегда имеют место силы инерции, так как вращение звена обязательно происходит с ускорением. Ускорение во вращательном движении раскладывается в общем случае на нормальную и касательную составляющие. Соответственно и сила инерции, равная произведению массы звена на ускорение его центра масс, может быть разложена на составляющие силы - нормальную и касательную. Опасной силой инерции при вращении звена является НОРМАЛЬНАЯ СИЛА. Если эта сила еще и не уравновешена, то ее вредное действие возрастает: кроме разрыва тела вращения, который может произойти при достижении этим телом определенной критической скорости, неуравновешенная сила инерции приводит к возникновению в опорных подшипниках звена добавочных динамических реакций. Неуравновешенная нормальная сила инерции не постоянна по направлению - она вращается вместе со звеном, вызывая раскачивание опор и нарушение в них режима трения. Неуравновешенные нормальные силы инерции вызывают шум, вибрации, а в момент резонанса могут привести к поломке машины. Нормальные силы инерции точечных масс, распределенных по звену, приводятся: 1. К нулю. 2. К силе (главному вектору). 3. К паре (главному моменту). 4. К силе и паре (винту). Если силы инерции приводятся к нулю, то звено уравновешено; к силе - не уравновешено статически; к паре - звено не уравновешено динамически; к силе и паре - смешанный случай неуравновешенности звена.  Схематично перечисленные случаи неуравновешенности показаны на рис. 1. Процесс выявления и устранения неуравновешенности звена называется б а л а н с и р о в к о й звена. В зависимости от вида неуравновешенности балансировка подразделяется на с т а т и ч е с к у ю и д и н а м и ч е с к у ю. При этом под динамической балансировкой понимают устранение как динамической (рис. 1, б), так и смешанной (рис. 1, в) неуравновешенности звена. Целью динамической балансировки является: 1. Выявление величины и плоскости действия момента неуравновешенных сил инерции звена. Устранение влияния этого момента путем изменения массы звена.
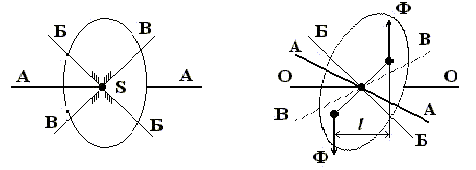
Рис. 1. Виды неуравновешенности: Звенья, имеющие форму тел вращения, проектируются уравновешенными. Однако при их изготовлении вносятся погрешности, которые могут привести к неуравновешенности звена - к несовпадению главной центральной оси инерции с осью вращения звена (главная центральная ось инерции проходит через центр масс звена; нормальных сил инерции относительно этой оси и любой другой, ей перпендикулярной, равен нулю). На рис. 2 изображено звено в форме круглого диска.
АА, ББ, ВВ - главные центральные оси инерции (S - центр масс звена). Оси ББ и ВВ лежат в плоскости диска, ось АА - ей перпендикулярна. При вращении диска вокруг любой из этих осей не будет возникать никаких моментов от нормальных сил инерции, или иначе - диск будет полностью уравновешен. На рис. 3 показан случай, когда ось О-О вращения диска является центральной осью инерции (проходит через центр масс), но не главной. Нормальные силы инерции точечных масс диска приводятся в этом случае к паре (главному моменту):
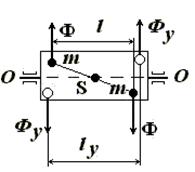
Главный вектор сил инерции равен нулю. В итоге диск оказывается неуравновешенным динамически (схема на рис. 1, б). В связи с тем, что центр массS диска находится на оси вращения, обнаружить динамическую неуравновешенность можно только при достаточно быстром вращении диска, когда становится заметным действие момента неуравновешенных сил инерции. Устранение динамической неуравновешенности диска заключается в совмещении главной центральной оси инерции АА с осью вращения ОО. На рис. 4 изображен вал с двумя неуравновешенными массами m, расположенными в одной осевой плоскости на одинаковом расстоянии от оси
вращения О-О. Развиваемые неуравновешенными массами m силы инерции образуют пару с моментом
действующим в осевой плоскости вала. Вал неуравновешен динамически, но уравновешен статически (центр масс S лежит на оси вращения). Уравновешивание вала достигается из условия равенства моментов сил инерции:
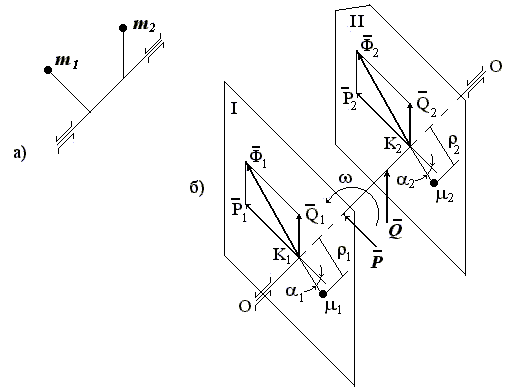
Противовесы следует устанавливать в плоскости расположения неуравновешенных масс m. Динамическую неуравновешенность вала (как и диска, рис. 3) также можно обнаружить только при его вращении, когда опять-таки проявляется действие в осевой плоскости вала момента неуравновешенных сил инерции. Рассмотрим теперь случай смешанной неуравновешенности вала и его балансировку (схема на рис. 1, в). Пусть имеются две неуравновешенные неодинаковые по величине массы m1 и m2, расположенные в разных плоскостях, как вращения, так и осевых (рис. 5, а). Нормальные силы инерции, развиваемые этими массами, обозначим соответственно P, Q (рис. 5,б). Для уравновешивания указанных сил инерции проведем через точки К1 и К2 перпендикулярно оси вращения две плоскости пл. I и пл. II. Эти плоскости называются плоскостями уравновешивания (точки К1 и К2 на оси вращения ОО выбраны произвольно).
Рис. 5. Схема вала с двумя неуравновешенными массами: |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 469. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
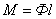 .
.
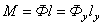 .
.