Схема аналізу ефективності підвищення ступеня многочлена у рівнянні поліноміальної регресії

Вихідні дані.

Дано радіус контуру живлення R_к=200 м, радіус свердловини r_с=0,1 м, дані промислових вимірів дебіту свердловини Q та депресії тиску Δр, що наведено у таблицях 9.3 і 9.4 (згідно з варіантом студента).

Таблиця 9.3

Таблиця 9.4

Хід роботи

1. У таблицю 9.5 заносимо дані промислових вимірів дебіту свердловини Q та депресії тиску Δр, а також проводимо відповідні розрахунки.

Таблиця 9.5

2. Побудуємо точковий графік залежності депресії тиску Δр від дебіту свердловини Q і проведемо лінію тренда (рис. 9.1).

Рис. 9.1. Графік залежності депресії тиску Δр від дебіту свердловини Q

Як видно, для умов прикладу лінійна функція Δр=1,2Q–4,1 досить непогано апроксимує результати промислових вимірів дебіту свердловини та депресії тиску.

Для уточнення проведених розрахунків скористаємося аналітичною залежністю депресії на пласт Δp та дебіту Q для гідродинамічно недосконалих свердловинах при спільній дії лінійного та нелінійного режимів фільтрації в пласті.

3. У гідродинамічно недосконалих свердловинах при спільній дії лінійного та нелінійного режимів фільтрації в пласті дебіт Q та депресія на пласт Δp пов’язані залежністю, що виражається многочленом другого ступеня:

де ε=k·h/μ – гідропровідність пласта, м³/(Па·с); h – ефективна (охоплена фільтрацією) товщина продуктивних пластів, м; k – проникність пластів для нафти, м²; μ – в’язкість нафти у пластових умовах, Па·с; R_к – радіус контуру живлення, м; r_с – радіус свердловини, м; ρ – густина нафти, кг/м³; m – пористість пласта; d_e – ефективний діаметр часток породи-колектору.

4. Позначаємо . Тоді .

Для лінеаризації цієї моделі поділимо обидві частини рівняння на Q, тоді: Z=Δр/Q=a₀+a₁Q (дані розрахунки заносимо у стовпчик 4 табл. 10.5).

5. Для визначення коефіцієнтів a₀ та a₁ складемо систему нормальних рівнянь у матричній формі (де N – кількість дослідів):

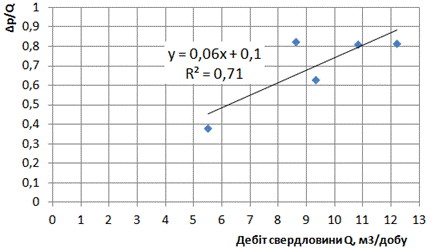
Для визначення коефіцієнтів a₀ та a₁ можливо також використати функцію «ЛИНЕЙН» чи функцію «Регрессия» пакета «Анализ данных».

Для умов прикладу функція регресії буде мати наступний вигляд Z=0,1+0,064Q.

6. Побудуємо точковий графік залежності Δр/Q від дебіту свердловини Q і проведемо лінію тренда (рис. 9.2).

Рис. 9.2. Графік залежності Δр/Q від дебіту свердловини Q

7. Визначаємо коефіцієнт кореляції для розрахованих коефіцієнтів функції регресії. Для цього рекомендуємо використати функцію «КОРРЕЛ» («массив1» – виділити стовпчик 2 табл. 9.4; «массив2» – виділити стовпчик 4 табл. 9.4).

Для вихідних даних прикладу коефіцієнт кореляції складає r=0,84>0,7. Отже, можна стверджувати, що між Δр/Q і Q існує високий кореляційний зв’язок, і ступінь наближення прямої регресії до фактичних промислових даних є також високою. Тому за допомогою цієї моделі можливо досить точно визначити гідропровідність пласта, яка становитиме:

Практичне заняття №10

Модель множинної регресії

Теоретичні відомості за темою практичної роботи.

Рівняння множинної регресії – рівняння залежності однієї величини Y (функції) від множини інших Х₁, Х₂, …, Х_m (аргументів).

Геометричним образом рівняння множинної регресії є гіперплощина – площина в m-вимірному просторі.

Для рівняння регресії величини Y=a₀+a₁Х₁+a₂Х₂ система нормальних рівнянь для оцінки коефіцієнтів регресії у матричному вигляді буде такою:

У разі збільшення кількості аргументів розмір системи нормальних рівнянь збільшується відповідно до кількості аргументів m і становить m+1. У матричній формі система нормальних рівнянь для лінійної регресії Y=a₀+a₁Х₁+a₂Х₂+…+a_mХ_m має наступний вигляд:

Схема дисперсійного аналізу множинної лінійної регресії наведено у таблиці 10.1.

Таблиця 10.1